题目内容
5.已知平面α⊥β,α∩β=m,n?β,则“n⊥m”是“n⊥α”成立的( )| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 利用面面垂直线面垂直判定和性质和充要条件的定义即可判断.
解答 解:由于α⊥β,α∩β=m,n?β,
若n⊥m,根据线面垂直的判断定理,则n⊥α,
若n⊥α,根据线面垂直的性质定理,则n⊥m,
故平面α⊥β,α∩β=m,n?β,则“n⊥m”是“n⊥α”成立充要条件.
故选:A.
点评 本题以线面垂直面面垂直为载体,考查了充分条件和必要的条件的判断,属于基础题.

练习册系列答案
相关题目
16.已知命题p:“?x∈R,ex-x-1≤0”,则命题¬p( )
| A. | ?x∈R,ex-x-1>0 | B. | ?x∉R,ex-x-1>0 | C. | ?x∈R,ex-x-1≥0 | D. | ?x∈R,ex-x-1>0 |
20.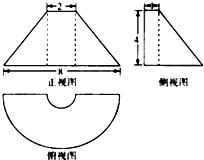 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
14.执行右面的程序框图,若输入x=7,y=6,则输出的有数对为( )
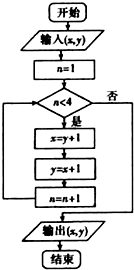

| A. | (11,12) | B. | (12,13) | C. | (13,14) | D. | (13,12) |
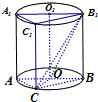 如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P
如图,圆柱OO1内接直三棱柱ABC-A1B1C1,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且AB=AA1.在圆柱OO1内随机选取一点,记该点取自于三棱柱ABC-A1B1C1内的概率为P