题目内容
12.设i是虚数单位,a为实数,复数z=$\frac{1+ai}{i}$为纯虚数,则z的共轭复数为( )| A. | -i | B. | i | C. | 2i | D. | -2i |
分析 利用复数代数形式的乘除运算化简,由实部为0求得a,则z可求,$\overline{z}$可求.
解答 解:由z=$\frac{1+ai}{i}$=$\frac{(1+ai)(-i)}{-{i}^{2}}=a-i$为纯虚数,得a=0,
∴z=-i,则$\overline{z}=i$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了共轭复数的概念,是基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
20.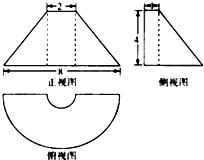 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
7.直线l:8x-6y-3=0被圆O:x2+y2-2x+a=0所截得弦的长度为$\sqrt{3}$,则实数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1-$\frac{{\sqrt{13}}}{2}$ |
1.设a∈R,且(a-i)•2i(i为虚数单位)为正实数,则a等于( )
| A. | 1 | B. | 0 | C. | -1 | D. | 0或-1 |
6.设全集U是实数集R,M={x|x>2或x<-2},N={x|x≥3或x<1},则(∁UM)∩N是( )
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
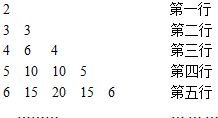
 根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015
根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015