题目内容
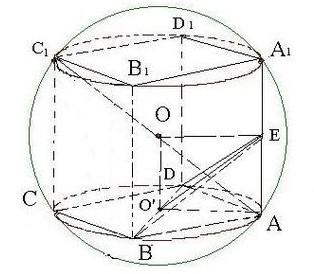
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8 | B.16 : : | C.14 | D.18 |
B.
试题分析:∵长方体ABCD—A1B1ClD1内接于球O,∴球心O是A
 中点。
中点。∵ABCD是边长为2的正方形,∴BD=2
 ,
,设BD中点为O‘,连接OO'
∴OO'⊥平面ABCD
∵E为A
 的中点,
的中点,∴AE//OO', AE=OO'
∴AO'OE为矩形
∵OA垂直平面BDE
∴OA⊥EO'
∴AO'OE为正方形
∴AO=
 AO'=2
AO'=2即球O的半径R=2
∴球O面积4πR²=16π,故选B。
点评:中档题,首先认定球心O是A
 中点,围绕球半径的计算,构造出现直角三角形,利用直角三角形的边角关系求解。
中点,围绕球半径的计算,构造出现直角三角形,利用直角三角形的边角关系求解。
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 中,
中, ,且
,且 ,
, 平面
平面 ,过
,过 作截面分别交
作截面分别交 于
于 ,且二面角
,且二面角 的大小为
的大小为 ,则截面
,则截面 面积的最小值为 .
面积的最小值为 .
 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则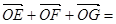 ( )
( )



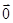


 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且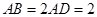 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 中,
中, 是棱
是棱 的中点.
的中点.
 平面
平面 ;
; .
. 的棱线长为1,线段
的棱线长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则三棱锥
,则三棱锥 的体积为
的体积为