题目内容
将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD成60°的角; ④AB与CD所成的角是60°.
其中正确结论的序号是________.
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD成60°的角; ④AB与CD所成的角是60°.
其中正确结论的序号是________.
①②④
试题分析:①取BD的中点O,连接OA,OC,所以
 ,所以
,所以 平面OAC,所以AC⊥BD;②设正方形的边长为a,则在直角三角形ACO中,可以求得OC=a,
平面OAC,所以AC⊥BD;②设正方形的边长为a,则在直角三角形ACO中,可以求得OC=a,所以△ACD是等边三角形;③AB与平面BCD成45角;④分别取BC,AC的中点为M,N,连接ME,NE,MN.则MN∥AB,且MN=
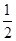 AB=
AB=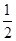 a,ME∥CD,且ME=
a,ME∥CD,且ME=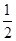 CD=
CD=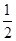 a,∴∠EMN是异面直线AB,CD所成的角.在Rt△AEC中,AE=CE=
a,∴∠EMN是异面直线AB,CD所成的角.在Rt△AEC中,AE=CE= a,AC=a,∴NE=
a,AC=a,∴NE=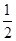 AC=
AC=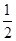 a.∴△MEN是正三角形,∴∠EMN=60°,故④正确.
a.∴△MEN是正三角形,∴∠EMN=60°,故④正确.点评:解决此类折叠问题,关键是搞清楚折叠前后的变量和不变的量.

练习册系列答案
相关题目
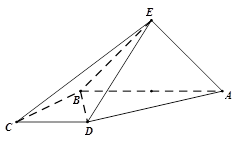
 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.

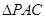 与
与 是均以
是均以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, ,
, 分别为
分别为 ,
, ,
, 为
为 的中点,且
的中点,且 平面
平面 .
.
 平面
平面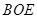 ;
; 的余弦值.
的余弦值.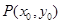
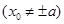 是双曲线
是双曲线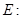
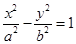
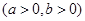 上一点,
上一点,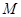 、
、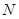 分别是双曲线
分别是双曲线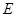 的左、右顶点,直线
的左、右顶点,直线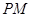 ,
,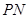 的斜率之积为
的斜率之积为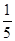 .
.
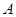 ,
,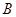 两点,
两点,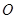 为坐标原点,
为坐标原点,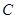 为双曲线上一点,满足
为双曲线上一点,满足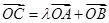 ,求
,求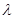 的值.
的值.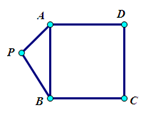
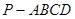 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.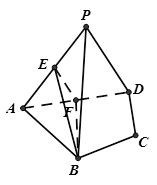
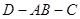 ,如图二,在二面角
,如图二,在二面角