Question

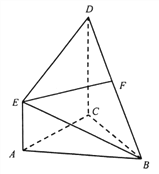
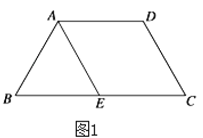
【题目】如图1，等腰梯形中，，是的中点.将沿折起后如图2，使二面角成直二面角，设是的中点，是棱的中

点.

（1）求证：；

（2）求证：平面平面；

（3）判断能否垂直于平面，并说明理由.

Answer 1

【答案】（1）答案见解析.（2）答案见解析（3）与平面不垂直，理由见解析

【解析】

（1）证明，只需证明平面，利用与E是等边三角形，即可证明；

（2）证明平面平面，只需证明平面，只需证明平面即可；

（3）与平面不垂直.假设平面，则，从而可证明平面，可得，这与矛盾.

（1）证明：设中点为，连接，

∵在等腰梯形中，，，，是的中点，∴与都是等边三角形.

∴，.

∵，平面，

∴平面.

∵平面，∴.

（2）证明：连接交于点，∵，，∴四边形是平行四边形，∴是线段的中点.

∵是的中点，∴.

∵平面，∴平面.

又∵平面，

∴平面平面.

（3）解：与平面不垂直.

证明：假设平面，则，∵平面，∴.

∵，平面，∴平面.

∵平面，∴，这与矛盾.

∴与平面不垂直.