Question

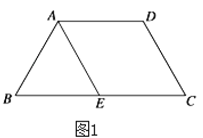
【题目】如图，多面体ABCDEF中，四边形ABCD为矩形，二面角A-CD-F为60°，DE∥CF，CD⊥DE，AD=2，DE=DC=3，CF=6.

（1）求证：BF∥平面ADE；

（2）在线段CF上求一点G，使锐二面角B-EG-D的余弦值为.

Answer 1

【答案】（1）详见解析；（2）点满足.

【解析】

（1）先证明平面，平面，可得平面平面，从而可得结果；（2）作于点，则平面，以平行于的直线为轴，所在直线为轴，所在直线为轴，建立空间直角坐标系，设，利用向量垂直数量积为零列方程组求得平面的法向量，结合面的一个法向量为，利用空间向量夹角余弦公式列方程解得，从而可得结果.

（1）因为ABCD是矩形，所以BC∥AD，

又因为BC不包含于平面ADE，

所以BC∥平面ADE，

因为DE∥CF，CF不包含于平面ADE，

所以CF∥平面ADE，

又因为BC∩CF＝C，所以平面BCF∥平面ADF，

而BF平面BCF，所以BF∥平面ADE．

（2）∵CD⊥AD，CD⊥DE

∴∠ADE为二面角A-CD-F的平面角

∴∠ADE=60°

∵CD⊥面ADE

平面平面，作于点，

则平面，

由，得，

以为原点，平行于的直线为轴，所在直线为轴，所在直线为轴，

建立如图所示的空间直角坐标系，

则，

，

设，则，

设平面的法向量为，

则由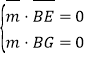，得，取，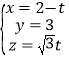

得平面的一个法向量为，

又面的一个法向量为，

，

，

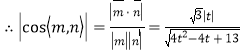解得或（舍去），

此时，得，

即所求线段上的点满足.