[题目]已知向量. .(1)若分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6).先后抛掷两次时第一次.第二次出现的点数.求满足的概率,(2)若在连续区间上取值.求满足的概率. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知向量， .

（1）若分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1,2,3,4,5,6），先后抛掷两次时第一次、第二次出现的点数，求满足的概率；

（2）若在连续区间上取值，求满足的概率.

【答案】(1) ;(2) 概率为.

【解析】试题分析：（1）本小题考査的知识点是古典概型，关键是要找出满足条件满足的基本事件个数，及总的基本事件的个数，再代入古典概型公式进行计算求解；（2）本小题考査的知识点是几何概型的意义，关键是要画出满足条件的图形，结合图形分析，找出满足条件的点集对应的图形面积，及图形的总面积.

试题解析：（1）将一枚质地均匀的正方体骰子先后抛掷两次时，所包含的基本事件总数为

个，由，有的基本事件有

故其概率为.

（2）若在连续区间上取值，则其全部基本事件的区域为，

满足的基本事件的区域为且，

如图，所求的概率即为梯形的面积，

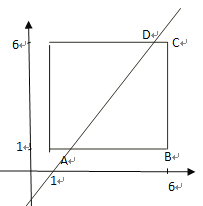
满足的概率为

练习册系列答案

相关题目

【题目】在各项均为正数的等比数列中，，且成等差数列.

（1）求等比数列的通项公式；

（2）若数列满足，求数列的前项和的最大值.

【题目】已知椭圆的中心在坐标原点，焦点在轴上，离心率，且椭圆经过点，过椭圆的左焦点且不与坐标轴垂直的直线交椭圆于，两点．

（1）求椭圆的方程；

（2）设线段的垂直平分线与轴交于点，求△的面积的取值范围．

【题目】已知圆，圆，动圆与圆内切并且与圆外切，圆心的轨迹为曲线.

（Ⅰ）求的方程；

（Ⅱ）已知曲线与轴交于两点，过动点的直线与交于 (不垂直轴)，过作直线交于点且交轴于点，若构成以为顶点的等腰三角形，证明：直线，的斜率之积为定值.

【题目】从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi(单位：千元)与月储蓄yi(单位：千元)的数据资料，算得＝80，＝20，＝184，＝720.

(1)求家庭的月储蓄y对月收入x的线性回归方程y＝bx＋a；

(2)判断变量x与y之间是正相关还是负相关；

(3)若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．

附：线性回归方程y＝bx＋a中，，a＝－b，其中，为样本平均值．

【题目】某保险公司有一款保险产品的历史收益率（收益率=利润÷保费收入）的频率分布直方图如图所示：

（Ⅰ）试估计平均收益率；

（Ⅱ）根据经验，若每份保单的保费在20元的基础上每增加元，对应的销量（万份）与（元）有较强线性相关关系，从历史销售记录中抽样得到如下5组与的对应数据：

据此计算出的回归方程为.

（i）求参数的估计值；

（ii）若把回归方程当作与的线性关系，用（Ⅰ）中求出的平均收益率估计此产品的收益率，每份保单的保费定为多少元时此产品可获得最大收益，并求出该最大收益.

【题目】选修4—5:不等式选讲

已知函数(x)=|2x-a|+ |x -1|.

（Ⅰ）当a=3时,求不等式(x)≥2的解集；

(Ⅱ)若(x)≥5-x对恒成立,求实数a的取值范围.

【题目】已知曲线y＝x＋ln x在点(1,1)处的切线与曲线y＝ax2＋(a＋2)x＋1相切，则a＝________

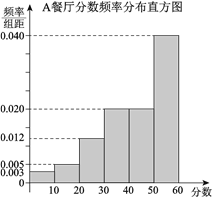
【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．

整理评分数据，将分数以为组距分成组：，，，，，，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：

B餐厅分数频数分布表
分数区间	频数

定义学生对餐厅评价的“满意度指数”如下：

分数
满意度指数

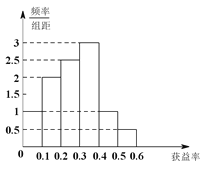
（Ⅰ）在抽样的100人中，求对A餐厅评价“满意度指数”为的人数；

（Ⅱ）从该校在A，B两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率；

（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

试题分类