题目内容
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
【答案】(1)a=-5,b=30 (2)![]() ,
,![]()
【解析】
(1)据题意可知,-3,2是方程ax2-5x+b=0的两实数根,由韦达定理即可求出a=-5,b=30;
(2)根据上面求得的a,b,得出A={x|30x2-5x-5>0},通过解不等式得出集合A,B,然后进行交集、并集和补集的运算即可.
(1)根据题意知,x=-3,2是方程ax2-5x+b=0的两实数根;
∴由韦达定理得,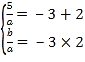 ;
;
解得a=-5,b=30;
(2)由上面,a=-5,b=30;
∴A={x|30x2-5x-5>0}=![]() ,且
,且![]() ;
;
∴![]() ,
,![]() ;
;
∴![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目