题目内容
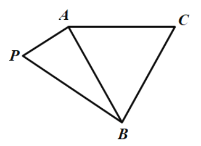
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
【答案】C
【解析】
对四个结论逐一分析判断,
对于①,利用翻折前后![]() 这个条件不变,易得
这个条件不变,易得![]() 平面
平面![]() ,从而
,从而![]() ;
;
对于②,当平面![]() 平面
平面![]() 时,四面体ABCD的体积最大,易得出体积;
时,四面体ABCD的体积最大,易得出体积;
对于③,当平面![]() 平面
平面![]() 时,BC与平面ABD所成的角最大,即
时,BC与平面ABD所成的角最大,即![]() ,计算其正弦值可得出结果;
,计算其正弦值可得出结果;
对于④,在翻折的过程中,BD的中点到四面体四个顶点的距离均相等,所以外接球的直径恒为BD,体积恒为定值.
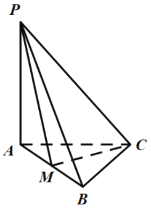
如图,当![]() 时,∵
时,∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,即①正确;
,即①正确;

当平面![]() 平面
平面![]() 时,四面体ABCD的体积最大,最大值为
时,四面体ABCD的体积最大,最大值为![]() ,即②正确;
,即②正确;
当平面![]() 平面
平面![]() 时,BC与平面ABD所成的角最大,为
时,BC与平面ABD所成的角最大,为![]() ,而
,而![]() ,
,
∴BC与平面ABD所成角一定小于![]() ,即③错误;
,即③错误;
在翻折的过程中,![]() 和
和![]() 始终是直角三角形,斜边都是BD,其外接球的球心永远是BD的中点,外接球的直径为BD,
始终是直角三角形,斜边都是BD,其外接球的球心永远是BD的中点,外接球的直径为BD,
∴四面体ABCD的外接球的体积不变,即④正确.
故正确的有①②④.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目