题目内容
【题目】若存在实数k,b,使得函数![]() 和
和![]() 对其定义域上的任意实数x同时满足:
对其定义域上的任意实数x同时满足:![]() 且
且![]() ,则称直线:
,则称直线:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中e为自然对数的底数).试问:
(其中e为自然对数的底数).试问:
(1)函数![]() 和
和![]() 的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数![]() 和
和![]() 是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
【答案】(1)存在,交点坐标为![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)构造函数![]() ,求导得到函数的单调区间,得到函数在
,求导得到函数的单调区间,得到函数在![]() 处取得最小值为0,得到答案.
处取得最小值为0,得到答案.
(2)设直线![]() ,根据
,根据![]() 得到
得到![]() ,再证明
,再证明![]() 恒成立,令
恒成立,令![]() ,求导得到单调区间,计算最值得到证明.
,求导得到单调区间,计算最值得到证明.
(1)∵![]() ,
,
∴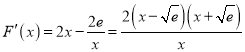 ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
故当![]() 时,
时,![]() 取到最小值,最小值是0,
取到最小值,最小值是0,
从而函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,交点坐标为
处有公共点,交点坐标为![]() .
.
(2)由(1)可知,函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,
处有公共点,
因此存在![]() 和
和![]() 的隔离直线,那么该直线过这个公共点,
的隔离直线,那么该直线过这个公共点,
设隔离直线的斜率为k,则隔离直线方程为![]() ,
,
即![]() ,
,
由![]() ,可得
,可得![]() 在
在![]() 上恒成立,
上恒成立,
则![]() ,只有
,只有![]() ,
,
此时直线方程为:![]() ,下面证明
,下面证明![]() 恒成立,
恒成立,
令![]() ,
,
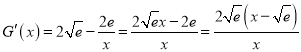 ,当
,当![]() 时,
时,![]() ,
,
当![]() 时
时![]() ,函数单调递减;
,函数单调递减;![]() 时,
时,![]() ,函数单调递增,
,函数单调递增,
则当![]() 时,
时,![]() 取到最小值是0,
取到最小值是0,
所以![]() ,则
,则![]() 当
当![]() 时恒成立.
时恒成立.
∴函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目