题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)证明:![]() ;
;
(Ⅲ)若![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
(Ⅰ)利用导数证明出不等式![]() 对任意的
对任意的![]() 恒成立,然后利用数学归纳法可证得
恒成立,然后利用数学归纳法可证得![]() ;
;
(Ⅱ)利用分析法,得出![]() ,然后构造函数
,然后构造函数![]() ,利用导数证明出
,利用导数证明出![]() 在区间
在区间![]() 上单调递增,进而可得出
上单调递增,进而可得出![]() ,即可证得结论;
,即可证得结论;
(Ⅲ)由(Ⅰ)(Ⅱ)可推导出![]() ,再由
,再由![]() 可得出
可得出![]() ,再利用放缩法结合等比数列的求和公式证明结论.
,再利用放缩法结合等比数列的求和公式证明结论.
(Ⅰ)设![]() ,其中
,其中![]() ,
,![]() ,
,
所以,函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() ,则
,则![]() .
.
再用数学归纳法证明![]() .
.
①因为![]() ,所以
,所以![]() ,由
,由![]() 知
知![]() ;
;
②假设当![]() 时,
时,![]() ,
,
则当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,
,
综上由①②知![]() 对一切
对一切![]() 恒成立;
恒成立;
(Ⅱ)要证![]() ,即证
,即证![]() ,其中
,其中![]() ,
,
令![]() ,则
,则![]() ,
,
所以,函数![]() 在区间
在区间![]() 上单调递增,从而
上单调递增,从而![]() ,
,
即![]() ,得证;
,得证;
(Ⅲ)由(Ⅰ)(Ⅱ)知,![]() .
.
因为当![]() 时,
时,![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
构造数列![]() ,则
,则![]() ,即
,即![]() ,
,
所以,数列![]() 从第
从第![]() 项开始单调递减,此时,
项开始单调递减,此时,![]() ,则
,则![]() ,
,
则![]() ,可得
,可得![]() ,
,
从而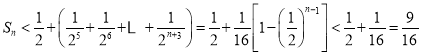 ,
,
又![]() 时,
时,![]() ,所以
,所以![]() 得证.
得证.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目