题目内容
【题目】设函数![]() (x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,
(x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,![]() ).
).
(Ⅰ)若f(x)≥0在x∈R上恒成立,求实数a的取值范围;
(Ⅱ)若ex≥lnx+m对任意x>0恒成立,求证:实数m的最大值大于2.3.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)分离参数,构造函数,利用导数求出函数的最值,问题得以解决;
(Ⅱ)构造函数设![]() ,利用导数求出函数的最值,即可证明.
,利用导数求出函数的最值,即可证明.
(Ⅰ)∵![]() ,f(x)≥0在x∈R上恒成立,∴a≤
,f(x)≥0在x∈R上恒成立,∴a≤![]() ,
,
设h(x)=![]() ,∴h′(x)=
,∴h′(x)=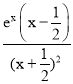 ,令h′(x)=0,解得x=
,令h′(x)=0,解得x=![]() ,
,
当x>![]() ,即h′(x)>0,函数单调递增,
,即h′(x)>0,函数单调递增,
当x<![]() ,即h′(x)<0,函数单调递减,
,即h′(x)<0,函数单调递减,
∴h(x)min=h(![]() )=
)=![]() ,∴0<a≤
,∴0<a≤![]() ,
,
故a的取值范围为![]() ;
;
(Ⅱ)设![]() ,
,
∴![]() ,g'(x)>0,可得
,g'(x)>0,可得![]() ;g'(x)<0,可得
;g'(x)<0,可得![]() .
.
∴g(x)在(![]() ,+∞)上单调递增;在
,+∞)上单调递增;在![]() 上单调递减.
上单调递减.
∴g(x)≥g(![]() )=
)=![]() ,∵
,∵![]() ,
,
∴![]() >1.6,∴g(x)>2.3.
>1.6,∴g(x)>2.3.
由(Ⅰ)可得ex![]() x
x![]() ,
,
∴ex﹣lnx的最小值大于2.3,
故若ex≥lnx+m对任意x>0恒成立,则m的最大值一定大于2.3.

【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.