题目内容
18．如图所示，某几何体的三视图相同，均为圆周的$\frac{1}{4}$，则该几何体的表面积为（ ）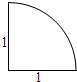
| A． | $\frac{3}{4}$π | B． | $\frac{5}{4}$π | C． | π | D． | 2π |
分析 根据三视图得出可以判断几何体是半径为1的球的$\frac{1}{8}$．运用数据得出该几何体的表面积为3×$\frac{1}{4}$×π×12+$\frac{1}{8}$×4×π×12=$\frac{5}{4}$π，
解答 解：∵某几何体的三视图相同，均为圆周的$\frac{1}{4}$，
∴可以判断几何体是半径为1的球的$\frac{1}{8}$．
∴该几何体的表面积为3×$\frac{1}{4}$×π×12+$\frac{1}{8}$×4×π×12=$\frac{5}{4}$π，
故选：B
点评 本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键，属于中档题．
练习册系列答案
相关题目
济南天下第一泉风景区为了做好宣传工作，准备在A和B两所大学分别招募8名和12名志愿者，将这20名志愿者的身高编成如右茎叶图（单位：cm）．若身高在175cm以上（包括175cm）定义为“高精灵”，身高在175cm以下 （不包括175cm）定义为“帅精灵”．已知A大学志愿者的身高的平均数为176cm，B大学志愿者的身高的中位数为168cm．
9．已知变量x，y满足的不等式组$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-2≥0}\end{array}\right.$表示的区域为D，B，C为区域D内的任意两点，设$\overrightarrow{OB}$，$\overrightarrow{OC}$的夹角为θ，则tanθ的最大值是（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{5}$ |
3．已知点A=（-1，1）、B=（1，2）、C=（-3，2），则向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为（ ）
| A． | -$\frac{3}{5}$ | B． | $\frac{3\sqrt{5}}{5}$ | C． | -$\frac{3\sqrt{5}}{5}$ | D． | $\frac{3}{5}$ |
15．从点P出发的三条射线PA，PB，PC两两成60°角，且分别与球O相切于A，B，C三点，若OP=$\sqrt{3}$，则球的体积为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{4π}{3}$ | D． | $\frac{8π}{3}$ |