题目内容
7.已知函数f(x)=xe-x+1.(1)求函数f(x)的单调区间;
(2)是否存在实数x,使得f(1-x)=f(x+1)?若存在,求出x的值;否则,说明理由;
(3)若存在不等实数x1、x2,使得f(x1)=f(x2),证明:f′($\frac{{x}_{1}+{x}_{2}}{2}$)<0.
分析 (1)求出导数,令导数大于0,得增区间,令导数小于0,得减区间;
(2)假设存在实数x,使得f(1-x)=f(x+1),化简整理,可得x=0成立;
(3)由于存在不等实数x1、x2,使得f(x1)=f(x2),即x1-lnx1=x2-lnx2,令g(x)=x-lnx,g(x1)=g(x2),
不妨设0<x1<1<x2,则2-x1>1,g(2-x1)-g(x2)=g(2-x1)-g(x1),化简整理,设F(t)=$\frac{2t-2}{1+t}$-lnt,求出导数,判断单调性,得到x1+x2>2,即可得证.
解答 解:(1)函数f(x)=xe-x+1的导数为f′(x)=(1-x)e1-x,
f′(x)>0可得x<1,f′(x)<0可得x>1,
则f(x)的增区间为(-∞,1);减区间为(1,+∞);
(2)假设存在实数x,使得f(1-x)=f(x+1),
即有(1-x)ex=(1+x)e-x,即e2x=$\frac{1+x}{1-x}$,
显然x=0时,上式成立;
当x>1时,显然不成立,
由$\frac{1+x}{1-x}$>0可得-1<x<1,
由e2x>$\frac{1+x}{1-x}$在(-1,0)成立,由e2x<$\frac{1+x}{1-x}$在(0,1)成立,
故存在实数x=0,使得f(1-x)=f(x+1);
(3)证明:由于存在不等实数x1、x2,使得f(x1)=f(x2),
即为x1${e}^{1-{x}_{1}}$=x2${e}^{1-{x}_{2}}$,即$\frac{{x}_{1}}{{x}_{2}}$=${e}^{{x}_{1}-{x}_{2}}$,
即有x1-x2=lnx1-lnx2,
即x1-lnx1=x2-lnx2,
令g(x)=x-lnx,g′(x)=1-$\frac{1}{x}$,
g(x1)=g(x2),
不妨设0<x1<1<x2,
则2-x1>1,
而g(2-x1)-g(x2)
=g(2-x1)-g(x1)
=(2-x1)-ln(2-x1)-x1+lnx1
=2-2x1-ln$\frac{2-{x}_{1}}{{x}_{1}}$,
令$\frac{2-{x}_{1}}{{x}_{1}}$=t,则t>1,x1=$\frac{2}{1+t}$,
故F(t)=$\frac{2t-2}{1+t}$-lnt,
故F′(t)=$\frac{-{t}^{2}+2t-1}{t(t+1)^{2}}$<0,
故F(t)在(1,+∞)上是减函数,
故F(t)<F(1)=0,
故g(2-x1)-g(x2)<0,
又∵g(x)在(1,+∞)上单调递增,
∴2-x1<x2,
故x1+x2>2,即$\frac{{x}_{1}+{x}_{2}}{2}$>1,
则有f′($\frac{{x}_{1}+{x}_{2}}{2}$)=(1-$\frac{{x}_{1}+{x}_{2}}{2}$)${e}^{1-\frac{{x}_{1}+{x}_{2}}{2}}$<0,
即为f′($\frac{{x}_{1}+{x}_{2}}{2}$)<0.
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查不等式的证明,注意运用构造函数,运用函数的单调性,考查运算能力,属于中档题.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案| 视力 | 4.6以下 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.0以上 |
| 人数(人) | 6 | 15 | 5 | 10 | 3 | 4 | 7 |
| A. | 4.6 | B. | 4.7 | C. | 4.8 | D. | 4.9 |
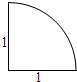
| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
| A. | 10,-10 | B. | 20,-20 | C. | 30,20 | D. | 30,10 |
 天猫电器城对海尔官方旗舰店某款4K超高清电视机在2015年1月11日的销售情况进行了统计,如图所示,数据显示,该日海尔官方旗舰店在[0,3)小时销售了该款电视机2台.
天猫电器城对海尔官方旗舰店某款4K超高清电视机在2015年1月11日的销售情况进行了统计,如图所示,数据显示,该日海尔官方旗舰店在[0,3)小时销售了该款电视机2台. 如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.
如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.