题目内容
9.已知变量x,y满足的不等式组$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-2≥0}\end{array}\right.$表示的区域为D,B,C为区域D内的任意两点,设$\overrightarrow{OB}$,$\overrightarrow{OC}$的夹角为θ,则tanθ的最大值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 由题意,画出平面区域,找出$\overrightarrow{OB}$,$\overrightarrow{OC}$的夹角为θ最大,时的位置,由数量积公式求夹角,得到tanθ的最大值.
解答 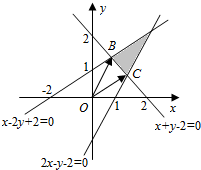 解:当B,C处于如图所示位置时,
解:当B,C处于如图所示位置时,
$\overrightarrow{OB}$,$\overrightarrow{OC}$的夹角为θ最大,得到B($\frac{2}{3},\frac{4}{3}$),C($\frac{4}{3},\frac{2}{3}$),则cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|}$=$\frac{\frac{2}{3}×\frac{4}{3}+\frac{4}{3}×\frac{2}{3}}{\sqrt{(\frac{2}{3})^{2}+(\frac{4}{3})^{2}}\sqrt{(\frac{4}{3})^{2}+(\frac{2}{3})^{2}}}=\frac{4}{5}$,所以0<θ<$\frac{π}{2}$,且sinθ=$\frac{3}{5}$,
因为tanθ在(0,$\frac{π}{2}$)是增函数,所以tanθ的最大值为$\frac{sinθ}{cosθ}$=$\frac{3}{4}$;
故选C.
点评 本题考查了线性规划问题中最值的求法;关键是正确画出平面区域,找出最值点.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
17.为了解九年级学生的视力情况,某校随机抽取50名学生进行视力检查,结果如表:
这组数据的中位数是( )?
| 视力 | 4.6以下 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.0以上 |
| 人数(人) | 6 | 15 | 5 | 10 | 3 | 4 | 7 |
| A. | 4.6 | B. | 4.7 | C. | 4.8 | D. | 4.9 |
4.以下四个命题中,正确的是( )
| A. | 在定义域内,只有终边相同的角的三角函数值才相等 | |
| B. | {α|α=k+$\frac{π}{6}$,k∈Z}≠{β|β=-k+$\frac{π}{6}$,k∈Z} | |
| C. | 若α是第二象限的角,则sin2α<0 | |
| D. | 第四象限的角可表示为{α|2k+$\frac{3}{2}$<α<2k,k∈Z} |
14.2014巴西足球世界杯最终以德国队高举大力神杯而落幕,专家认为:“中国的孩子既没时间也没场地踢球,现在急需足球这样的全民健身运动,当从民族的高度、战略的高度发展足球”,以下是某新闻媒体进行的网上调查,所有参与调查的人中,持“支持”、“中立”和“不支持”态度的人数如下表所示:
在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持”态度的人中抽取了45人,则n=100.
| 支持 | 中立 | 不支持 | |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
1.设函数f(x)是定义在R上的奇函数,当x∈(0,1]时,f(x)=x+3,则f(-$\frac{1}{2}$)=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
18.如图所示,某几何体的三视图相同,均为圆周的$\frac{1}{4}$,则该几何体的表面积为( )
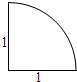

| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
 如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm.
如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm.