题目内容
13.以x轴正半轴为极轴建立极坐标系.已知射线l:θ=$\frac{π}{4}$与曲线C:$\left\{\begin{array}{l}{x=t+1}\\{y=(t-1)^{2}}\end{array}\right.$(t为参数)相交于A,B两点.(1)写出射线l的直角坐标方程和曲线C的普通方程;
(2)求线段AB的中点的极坐标.
分析 (1)射线l:θ=$\frac{π}{4}$的直角坐标方程为y=x(x≥0).把曲线C:$\left\{\begin{array}{l}{x=t+1}\\{y=(t-1)^{2}}\end{array}\right.$(t为参数),消去参数t,化为直角坐标方程.
(2)直线方程与抛物线方程联立解得交点A,B,利用中点坐标公式可得AB的中点.
解答 解:(1)射线l:θ=$\frac{π}{4}$的直角坐标方程为y=x(x≥0).
把曲线C:$\left\{\begin{array}{l}{x=t+1}\\{y=(t-1)^{2}}\end{array}\right.$(t为参数),消去参数t,化为直角坐标方程为y=(x-2)2.
(2)联立$\left\{\begin{array}{l}{y=x}\\{y=(x-2)^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
∴A(1,1),B(4,4),
故AB的中点为$(\frac{5}{2},\frac{5}{2})$,
化为极坐标为$(\frac{5\sqrt{2}}{2},\frac{π}{4})$.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、曲线的交点坐标,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
3.执行如图所示的程序框图,若输入k的值为2,则输出的i值为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.以下四个命题中,正确的是( )
| A. | 在定义域内,只有终边相同的角的三角函数值才相等 | |
| B. | {α|α=k+$\frac{π}{6}$,k∈Z}≠{β|β=-k+$\frac{π}{6}$,k∈Z} | |
| C. | 若α是第二象限的角,则sin2α<0 | |
| D. | 第四象限的角可表示为{α|2k+$\frac{3}{2}$<α<2k,k∈Z} |
1.设函数f(x)是定义在R上的奇函数,当x∈(0,1]时,f(x)=x+3,则f(-$\frac{1}{2}$)=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
18.如图所示,某几何体的三视图相同,均为圆周的$\frac{1}{4}$,则该几何体的表面积为( )
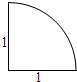

| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
5.定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,已知函数f(x)=$|\begin{array}{l}{π}&{x+1}\\{x-1}&{x}\end{array}|$,且△ABC是锐角三角形,则下列不等式成立的是( )
| A. | f(sinA)>f(sinB) | B. | f(cosA)>f(cosB) | C. | f(sinA)>f(cosB) | D. | f(cosA)>f(sinB) |
2.某地一天从6-14时的温度变化满足y=10sin($\frac{π}{8}$t+$\frac{3π}{4}$)+20,t∈[6,14],则最高气温和最低气温分别是( )
| A. | 10,-10 | B. | 20,-20 | C. | 30,20 | D. | 30,10 |
10.复数z1,z2满足|z1|=|z2|=1,|z1+z2|=$\sqrt{3}$,则|z1-z2|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |