题目内容
8. 济南天下第一泉风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高编成如右茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高精灵”,身高在175cm以下 (不包括175cm)定义为“帅精灵”.已知A大学志愿者的身高的平均数为176cm,B大学志愿者的身高的中位数为168cm.
济南天下第一泉风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高编成如右茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高精灵”,身高在175cm以下 (不包括175cm)定义为“帅精灵”.已知A大学志愿者的身高的平均数为176cm,B大学志愿者的身高的中位数为168cm.(Ⅰ)求x,y的值;
(Ⅱ)如果用分层抽样的方法从“高精灵”和“帅精灵”中抽取5人,再从这5人中选2人.求至少有一人为“高精灵”的概率.
分析 (I)根据求平均数及中位数的方法,即可求解x,y.
(II)根据分层抽样方法求得抽到的“高精灵”和“帅精灵”的志愿者人数,再分类求得至少有1人是“高精灵”的抽法种数与从这5人中选2人的种数,代入古典概型概率公式计算.
解答 解:(I)由茎叶图得:$\frac{159+168+170+x+176+182+187+191}{8}=176$,(2分)
$\frac{160+y+169}{2}=176$(4分)
解得,x=5,y=7(5分)
(II)由题意可得,高精灵有8人,帅精灵有12人,如果从“高精灵”和“帅精灵”中抽取5人,则“高精灵”和“帅精灵”的人数分别为:
$8×\frac{5}{20}=2$,$12×\frac{5}{20}$=3(6分)
记抽取的高精灵分别为b1,b2,帅精灵为c1,c2,c3,
从已经抽取的5人中任选2人的所有可能为:(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3)共10种结果(8分)
记从这5人中选2人.求至少有一人为“高精灵”为事件A,则A包括,(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3)共7种(10分)
∴$P(A)=\frac{7}{10}$
因此,如果用分层抽样的方法从“高精灵”和“帅精灵”中抽取5人,再从这5人中选2人,至少有一人为“高精灵的概率为$\frac{7}{10}$(12分)
点评 本题考查了利用茎叶图求平均数及中位数,考查分层抽样方法及古典概型的概率计算,要注意求至少有1人是“高精灵”的选法可用分类法,解答本题的关键是读懂茎叶图

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
3.执行如图所示的程序框图,若输入k的值为2,则输出的i值为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.为了解九年级学生的视力情况,某校随机抽取50名学生进行视力检查,结果如表:
这组数据的中位数是( )?
| 视力 | 4.6以下 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.0以上 |
| 人数(人) | 6 | 15 | 5 | 10 | 3 | 4 | 7 |
| A. | 4.6 | B. | 4.7 | C. | 4.8 | D. | 4.9 |
18.如图所示,某几何体的三视图相同,均为圆周的$\frac{1}{4}$,则该几何体的表面积为( )
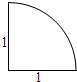

| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
 如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm.
如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm.