题目内容
3.已知点A=(-1,1)、B=(1,2)、C=(-3,2),则向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为( )| A. | -$\frac{3}{5}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | -$\frac{3\sqrt{5}}{5}$ | D. | $\frac{3}{5}$ |
分析 由已知可求$\overrightarrow{AB}$,$\overrightarrow{AC}$的坐标,根据$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为:$|\overrightarrow{AB}|cosθ$=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AC}|}$(θ为向量的夹角),即可求解.
解答 解:由已知可得,$\overrightarrow{AB}$=(2,1),$\overrightarrow{AC}$=(-2,1),
∴$\overrightarrow{AB}•\overrightarrow{AC}$=2×(-2)+1×1=-3,|$\overrightarrow{AC}$|=$\sqrt{5}$,
设$\overrightarrow{AB}$,$\overrightarrow{AC}$的夹角为θ,
则向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为:$|\overrightarrow{AB}|cosθ$=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AC}|}$=$\frac{-3}{\sqrt{5}}=-\frac{3\sqrt{5}}{5}$.
故选:C.
点评 本题主要考查了向量投影定义的简单应用,属于基础试题.

练习册系列答案
相关题目
14.2014巴西足球世界杯最终以德国队高举大力神杯而落幕,专家认为:“中国的孩子既没时间也没场地踢球,现在急需足球这样的全民健身运动,当从民族的高度、战略的高度发展足球”,以下是某新闻媒体进行的网上调查,所有参与调查的人中,持“支持”、“中立”和“不支持”态度的人数如下表所示:
在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持”态度的人中抽取了45人,则n=100.
| 支持 | 中立 | 不支持 | |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
18.如图所示,某几何体的三视图相同,均为圆周的$\frac{1}{4}$,则该几何体的表面积为( )
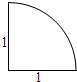

| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
8.二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是( )
| A. | 0<t<1 | B. | 0<t<2 | C. | 1<t<2 | D. | -1<t<1 |
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线与圆C:x2+y2-6x+1=0相交于A,B两点,且|AB|=4,则该双曲线离心率等于( )
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
20.已知原命题:“若a+b≥2,则a,b 中至少有一个不小于1”,则原命题与其否命题的真假情况是( )
| A. | 原命题为真,否命题为假 | B. | 原命题为假,否命题为真 | ||
| C. | 原命题与否命题均为真命题 | D. | 原命题与否命题均为假命题 |
 天猫电器城对海尔官方旗舰店某款4K超高清电视机在2015年1月11日的销售情况进行了统计,如图所示,数据显示,该日海尔官方旗舰店在[0,3)小时销售了该款电视机2台.
天猫电器城对海尔官方旗舰店某款4K超高清电视机在2015年1月11日的销售情况进行了统计,如图所示,数据显示,该日海尔官方旗舰店在[0,3)小时销售了该款电视机2台.