题目内容
15.从点P出发的三条射线PA,PB,PC两两成60°角,且分别与球O相切于A,B,C三点,若OP=$\sqrt{3}$,则球的体积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{8π}{3}$ |
分析 利用几何图形得出△ABC和△PAB为正三角形,根据正三角形的几何性质得出$\frac{OP}{OA}$=$\frac{AP}{A{O}^{′}}$,$\frac{A{O}^{′}}{AB}$=$\frac{\sqrt{3}}{3}$,
再直角三角形的几何性质得出$\frac{A{O}^{′}}{AP}$=$\frac{\sqrt{3}}{3}$所以OA=$\frac{OP•{O}^{′}A}{AP}$整体求解即可,得出半径求解球的体积.
解答 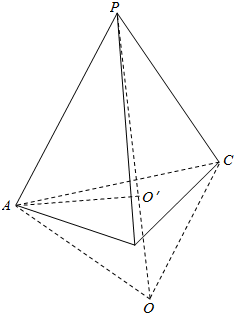 解:
解:
连接OP交平面ABC于O′,
由题意可得:△ABC和△PAB为正三角形,
所以O'A=$\frac{\sqrt{3}}{3}$AB=$\frac{\sqrt{3}}{3}$AP.因为AO'⊥PO,OA⊥PA,
所以$\frac{OP}{OA}$=$\frac{AP}{A{O}^{′}}$,$\frac{A{O}^{′}}{AB}$=$\frac{\sqrt{3}}{3}$,
$\frac{A{O}^{′}}{AP}$=$\frac{\sqrt{3}}{3}$
所以OA=$\frac{OP•{O}^{′}A}{AP}$=$\sqrt{3}×\frac{\sqrt{3}}{3}$=1,
球的半径为1,
故体积为$\frac{4}{3}$×π×13=$\frac{4}{3}$π,
故选:C
点评 本题考查空间中两点之间的距离,解决此类问题的方法是熟练掌握几何体的结构特征,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.如图所示,某几何体的三视图相同,均为圆周的$\frac{1}{4}$,则该几何体的表面积为( )
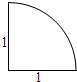

| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
10.复数z1,z2满足|z1|=|z2|=1,|z1+z2|=$\sqrt{3}$,则|z1-z2|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
20.已知原命题:“若a+b≥2,则a,b 中至少有一个不小于1”,则原命题与其否命题的真假情况是( )
| A. | 原命题为真,否命题为假 | B. | 原命题为假,否命题为真 | ||
| C. | 原命题与否命题均为真命题 | D. | 原命题与否命题均为假命题 |
7.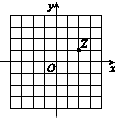 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )| A. | -$\frac{3}{5}$i | B. | -i | C. | $\frac{3}{5}$i | D. | i |
5.要得到函数y=sin(4x-$\frac{π}{3}$)的图象,只需要将函数y=sin4x的图象( )个单位.
| A. | 向左平移$\frac{π}{12}$ | B. | 向右平移$\frac{π}{12}$ | C. | 向左平移$\frac{π}{3}$ | D. | 向右平移$\frac{π}{3}$ |
 如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.
如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.