题目内容
(12分)如图,设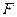 是椭圆
是椭圆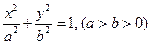 的左焦点,直线
的左焦点,直线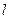 为对应的准线,直线
为对应的准线,直线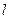 与
与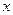 轴交于
轴交于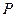 点,
点,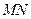 为椭圆的长轴,已知
为椭圆的长轴,已知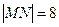 ,且
,且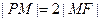 .
.
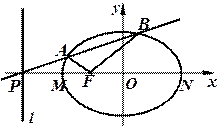 (1)求椭圆的标准方程;(2)求证:对于任意的割线
(1)求椭圆的标准方程;(2)求证:对于任意的割线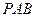 ,恒有
,恒有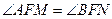 ;
;
(3)求三角形△ABF面积的最大值.
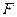 是椭圆
是椭圆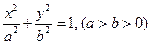 的左焦点,直线
的左焦点,直线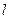 为对应的准线,直线
为对应的准线,直线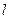 与
与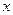 轴交于
轴交于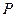 点,
点,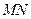 为椭圆的长轴,已知
为椭圆的长轴,已知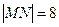 ,且
,且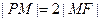 .
.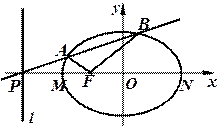 (1)求椭圆的标准方程;(2)求证:对于任意的割线
(1)求椭圆的标准方程;(2)求证:对于任意的割线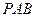 ,恒有
,恒有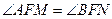 ;
;(3)求三角形△ABF面积的最大值.
(Ⅰ)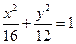 (Ⅱ)略 (Ⅲ)
(Ⅱ)略 (Ⅲ)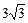
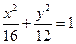 (Ⅱ)略 (Ⅲ)
(Ⅱ)略 (Ⅲ)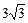
(1)∵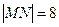 ,∴
,∴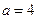 ,又∵
,又∵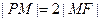 ,∴
,∴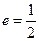 ,
,
∴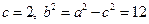 ,∴椭圆的标准方程为
,∴椭圆的标准方程为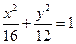 .---(4分)
.---(4分)
(2)当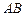 的斜率为0时,显然
的斜率为0时,显然 =0,满足题意,
=0,满足题意,
当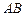 的斜率不为0时,设
的斜率不为0时,设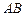 方程为
方程为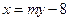 ,
,
代入椭圆方程整理得: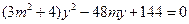 .
.
 ,
,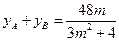 ,
,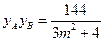 .----------------------------6分
.----------------------------6分
则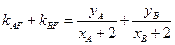
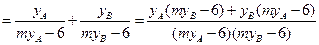
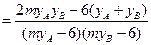 ,
,
而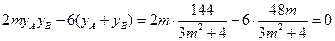
∴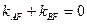 ,从而
,从而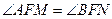 .
.
综合可知:对于任意的割线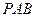 ,恒有
,恒有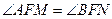 .………------------------(8分)
.………------------------(8分)
(3)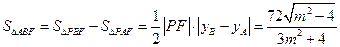 ,
,
即: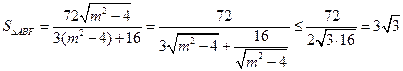 ,
,
当且仅当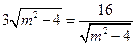 ,
,
即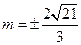 (此时适合于
(此时适合于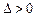 的条件)取到等号.
的条件)取到等号.
∴三角形△ABF面积的最大值是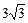 .……--(12分)
.……--(12分)
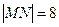 ,∴
,∴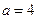 ,又∵
,又∵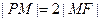 ,∴
,∴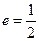 ,
,∴
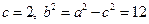 ,∴椭圆的标准方程为
,∴椭圆的标准方程为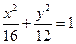 .---(4分)
.---(4分)(2)当
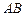 的斜率为0时,显然
的斜率为0时,显然 =0,满足题意,
=0,满足题意,当
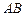 的斜率不为0时,设
的斜率不为0时,设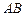 方程为
方程为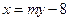 ,
,代入椭圆方程整理得:
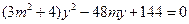 .
. ,
,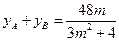 ,
,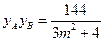 .----------------------------6分
.----------------------------6分则
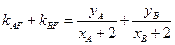
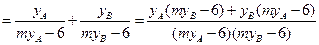
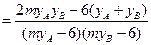 ,
,而
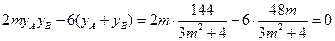
∴
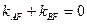 ,从而
,从而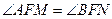 .
.综合可知:对于任意的割线
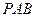 ,恒有
,恒有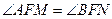 .………------------------(8分)
.………------------------(8分)(3)
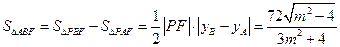 ,
,即:
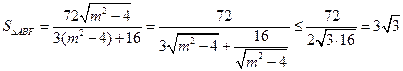 ,
,当且仅当
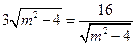 ,
,即
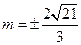 (此时适合于
(此时适合于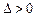 的条件)取到等号.
的条件)取到等号.∴三角形△ABF面积的最大值是
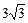 .……--(12分)
.……--(12分)
练习册系列答案
相关题目
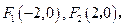 点
点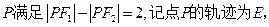
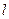 绕点
绕点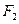 怎样转动,在
怎样转动,在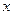 轴上总存在定点
轴上总存在定点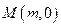 ,使
,使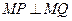 恒成立,求实数
恒成立,求实数 的值;
的值;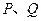 作直线
作直线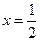 的垂线
的垂线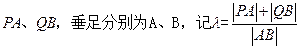
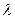 的取值范围
的取值范围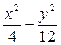 =-1的焦点为顶点,顶点为焦点的椭圆方程为( )
=-1的焦点为顶点,顶点为焦点的椭圆方程为( ) =1
=1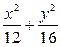 =1
=1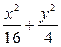 =1
=1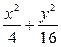 =1
=1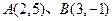 ,则线段AB的方程为( )
,则线段AB的方程为( )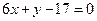
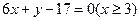
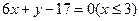
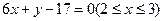
 )、N(-4,-
)、N(-4,-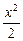 +y2="1," ④
+y2="1," ④

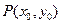 在椭圆
在椭圆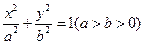 上,
上,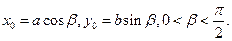 直线
直线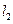 与直线
与直线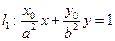 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为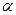 ,直线
,直线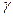 .
.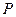 是椭圆
是椭圆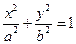 与直线
与直线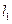 的唯一交点;
的唯一交点; 
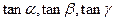 构成等比数列.
构成等比数列.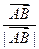 在向量
在向量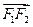 方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.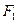 、
、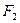 分别是椭圆
分别是椭圆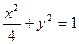 的左、右焦点.
的左、右焦点.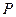 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求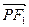 ·
·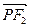 的最大值和最小值;
的最大值和最小值;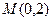 的直线
的直线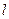 与椭圆交于不同的两点
与椭圆交于不同的两点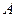 、
、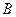 ,且∠
,且∠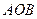 为锐角(其中
为锐角(其中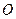 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围.