题目内容
已知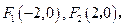 点
点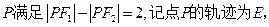
(1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点,
①无论直线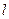 绕点
绕点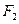 怎样转动,在
怎样转动,在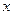 轴上总存在定点
轴上总存在定点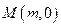 ,使
,使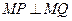 恒成立,求实数
恒成立,求实数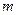 的值;
的值;
②过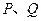 作直线
作直线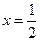 的垂线
的垂线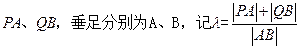
求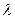 的取值范围
的取值范围
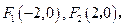 点
点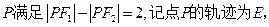
(1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点,
①无论直线
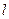 绕点
绕点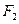 怎样转动,在
怎样转动,在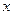 轴上总存在定点
轴上总存在定点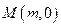 ,使
,使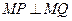 恒成立,求实数
恒成立,求实数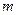 的值;
的值;②过
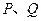 作直线
作直线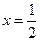 的垂线
的垂线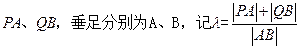
求
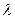 的取值范围
的取值范围(1)由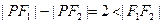 知,点
知,点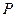 的轨迹
的轨迹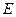 是以
是以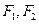 为焦点的双曲线右支,由
为焦点的双曲线右支,由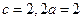 得
得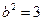 ,故轨迹
,故轨迹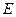 的方程为
的方程为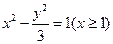 3分
3分
(2)当直线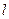 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为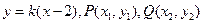
与双曲线方程联立消去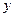 得:
得:
∴ ,解得
,解得 ………………5分
………………5分
①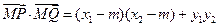

∵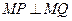 ,∴
,∴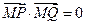 ,
,
故得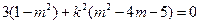 对任意的
对任意的 恒成立,
恒成立,
∴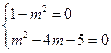 ,解得
,解得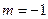 ,∴当
,∴当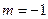 时,
时,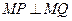 ……………8分
……………8分
当直线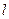 的斜率不存在时,由
的斜率不存在时,由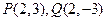 及
及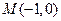 知结论也成立
知结论也成立
综上,当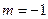 时,
时,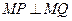 ……………9分
……………9分
②∵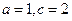 ,∴直线
,∴直线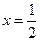 是双曲线右准线,
是双曲线右准线,
由双曲线定义得
∴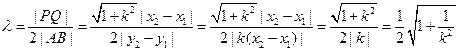
∵ ,∴
,∴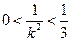 ,故
,故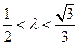
注意到直线的斜率不存在时, ,此时
,此时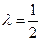
综上, ……………14分
……………14分
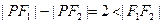 知,点
知,点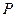 的轨迹
的轨迹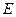 是以
是以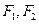 为焦点的双曲线右支,由
为焦点的双曲线右支,由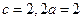 得
得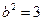 ,故轨迹
,故轨迹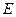 的方程为
的方程为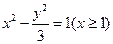 3分
3分(2)当直线
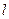 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为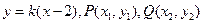
与双曲线方程联立消去
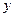 得:
得:
∴
 ,解得
,解得 ………………5分
………………5分①
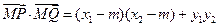

∵
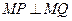 ,∴
,∴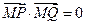 ,
,故得
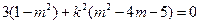 对任意的
对任意的 恒成立,
恒成立,∴
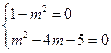 ,解得
,解得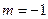 ,∴当
,∴当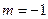 时,
时,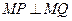 ……………8分
……………8分当直线
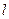 的斜率不存在时,由
的斜率不存在时,由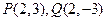 及
及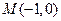 知结论也成立
知结论也成立综上,当
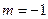 时,
时,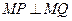 ……………9分
……………9分②∵
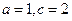 ,∴直线
,∴直线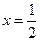 是双曲线右准线,
是双曲线右准线,由双曲线定义得

∴
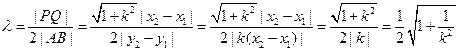
∵
 ,∴
,∴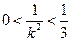 ,故
,故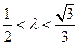
注意到直线的斜率不存在时,
 ,此时
,此时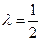
综上,
 ……………14分
……………14分同答案

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 为抛物线
为抛物线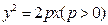 的顶点,
的顶点,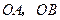 为这条抛物线互相垂直的两条动弦.
为这条抛物线互相垂直的两条动弦.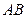 必过一定点.
必过一定点.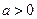 ,在矩形
,在矩形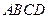 中,
中,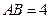 ,
,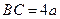 ,
,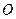 为
为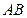 的中点.点
的中点.点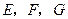 分别在
分别在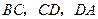 上移动,且
上移动,且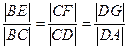 ,
, 为
为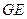 与
与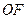 的交点(如图).问是否存在两个定点,使点
的交点(如图).问是否存在两个定点,使点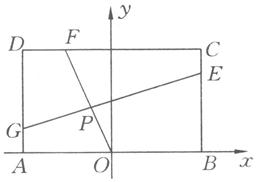
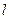 交椭圆
交椭圆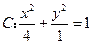 于
于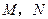 两点,且
两点,且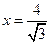 的距离之和为
的距离之和为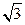 ,求直线
,求直线

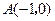 ,点
,点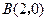 ,在第一象限的动点
,在第一象限的动点 满足
满足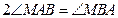 ,求点
,求点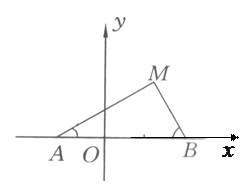
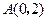 的距离减去它到
的距离减去它到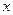 轴的距离的差是
轴的距离的差是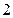 ,求这曲线的方程.
,求这曲线的方程.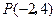 ,倾斜角为
,倾斜角为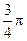 的直线
的直线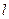 与抛物线
与抛物线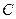 相交于
相交于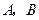 两点,抛物线
两点,抛物线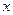 轴为对称轴,若
轴为对称轴,若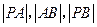 成等比数列,求抛物线
成等比数列,求抛物线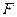 是椭圆
是椭圆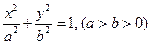 的左焦点,直线
的左焦点,直线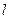 为对应的准线,直线
为对应的准线,直线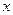 轴交于
轴交于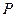 点,
点,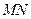 为椭圆的长轴,已知
为椭圆的长轴,已知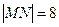 ,且
,且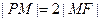 .
.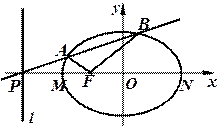 (1)求椭圆的标准方程;(2)求证:对于任意的割线
(1)求椭圆的标准方程;(2)求证:对于任意的割线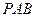 ,恒有
,恒有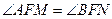 ;
;