题目内容
2.已知α是第二象限角,求$\frac{α}{2},\frac{α}{3}$是第几象限角.分析 根据α是第二象限角,写出α的取值范围,再求出$\frac{α}{2}$与$\frac{α}{3}$的取值范围.
解答 解:∵α是第二象限角,
∴$\frac{π}{2}$+2kπ<α<π+2kπ,k∈Z;
∴$\frac{π}{4}$+kπ<$\frac{α}{2}$<$\frac{π}{2}$+kπ,k∈Z,
∴k为偶数时,$\frac{α}{2}$是第一象限角,k为奇数时,$\frac{α}{2}$是第三象限角,
即$\frac{α}{2}$是第一、三象限角;
又$\frac{π}{6}$+$\frac{2}{3}$kπ<$\frac{α}{3}$<$\frac{π}{3}$+$\frac{2}{3}$kπ,k∈Z;
当k=3n,n∈Z时,$\frac{α}{3}$是第一象限角,
当k=3n+1,n∈Z时,$\frac{α}{3}$是第二象限角,
当k=3n+2,n∈Z时,$\frac{α}{3}$是第四象限角,
即$\frac{α}{3}$是第一、二、四象限角.
点评 本题考查了象限角的概念,解题时应明确象限角、轴线角的概念是什么,是基础题目.

练习册系列答案
相关题目
7.已知函数y=f(x)=$\left\{\begin{array}{l}{5x,0<x≤13}\\{7x+2,x>13}\end{array}\right.$的定义域是( )
| A. | (0.+∞) | B. | (-∞,0]∪[0,+∞) | C. | (-∞,0]∪(0,+∞) | D. | [0,+∞) |
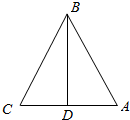 如图所示,△ABC中,AC=10cm,AC边上的高BD=10cm,求其水平放置的直观图的面积.
如图所示,△ABC中,AC=10cm,AC边上的高BD=10cm,求其水平放置的直观图的面积.