题目内容

2．如图所示是一个几何体的三视图，则这个几何体外接球的表面积为12π．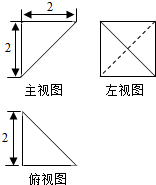

分析 几何体是三棱锥，结合直观图判断三棱锥的结构特征，根据三视图的数据求得外接球的半径，代入球的表面积公式计算．

解答 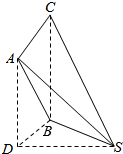解：由三视图知：几何体是三棱锥，如图三棱锥S=ABC，
其中SD⊥平面ACBD，四边形ACBD为边长为2的正方形，SD=2，
外接球的球心为SC的中点，
∴外接球的半径R=$\frac{\sqrt{4+4+4}}{2}$=$\sqrt{3}$，
∴外接球的表面积S=4π×3=12π．
故答案为：12π．

点评 本题考查了由三视图求几何体的外接球的表面积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．

练习册系列答案
相关题目
12．已知α，β是两个平面，直线l?α，l?β，若以①l⊥α，②l∥β，③α⊥β中两个为条件，另一个为结论构成三个命题，其中 正确的命题是（　　）
A．①③⇒②，①②⇒③B．①③⇒②，②③⇒①C．①②⇒③，②③⇒①D．①③⇒②，①②⇒③，②③⇒①
13．设抛物线C1：y2=4x的焦点为F，动点D到点F的距离与到直线x=4的距离之比为$\frac{1}{2}$．
（1）求动点D的轨迹C2的方程；
（2）过点F作直线l与曲线C2交于P、Q两点，A1，A2为C2与x轴的交点，直线PA1，QA2相交于点M，直线PA2，QA1相交于点N，求证：MF⊥NF．
10．已知点$A（1{，_{\;}}\sqrt{2}）$是离心率为$\frac{{\sqrt{2}}}{2}$的椭圆$\frac{x^2}{b^2}+\frac{y^2}{a^2}$=1（a＞b＞0）上的一点，斜率为$\sqrt{2}$的直线BC交椭圆于B、C两点，且B、C与A点均不重合．
（Ⅰ）求椭圆的方程；
（Ⅱ）△ABC的面积是否存在着最大值？若存在，求出这个最大值；若不存在，请说明理由？
（Ⅲ）求直线AB与直线AC斜率的比值．
17．2015年中国男子国家足球队再度征战世界杯亚洲区预选赛，中国队与卡塔尔、马尔代夫、不丹、中国香港同处一组．比赛采取主客场积分制，既任意两队分别在自己的国家或地区（主场）和对方的国家或地区（客场）各比赛一场，规定每场胜者得3分，负者得0分，战平各得1分，按积分多少排名．卡塔尔队是中国队最主要的竞争对手，假设中国队与卡塔尔队在对阵其他三队的主客场比赛中都全部获胜；中国队在对阵卡塔尔队主场战胜的概率为$\frac{1}{2}$，战平的概率为$\frac{1}{3}$，在客场胜、平、负的概率均为$\frac{1}{3}$，各场比赛结果相互独立．
（Ⅰ）求中国队在主场不败的情况下积分大于卡塔尔队积分的概率；
（Ⅱ）求比赛结束时中国队积分X的分布列与数学期望．
7．一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的表面积是（　　）
A．16$\sqrt{2}$+16πB．16$\sqrt{2}$+8πC．8$\sqrt{2}$+8πD．8$\sqrt{2}$+16π
14．已知函数f（x）（x∈R）是偶函数，函数f（x-2）是奇函数，且f（1）=1，则f（2015）=（　　）
A．2015B．-2015C．1D．-1
11．给出下列命题：①若$\overrightarrow a$•$\overrightarrow b$＜0，则$\overrightarrow a$、$\overrightarrow b$的夹角为钝角；②若$\overrightarrow a$=（x1，y1），$\overrightarrow b$=（x2，y2），则$\overrightarrow a$∥$\overrightarrow b$?$\frac{x_1}{x_2}$=$\frac{y_1}{y_2}$；③若{${\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$}为空间的一组基底，则对于实数x、y、z满足x$\overrightarrow a$+y$\overrightarrow b$+z$\overrightarrow c$=$\overrightarrow 0$时，x2+y2+z2=0；④|$\overrightarrow p$+$\overrightarrow q$|•|$\overrightarrow p$-$\overrightarrow q$|=|${\overrightarrow p^2}$-${\overrightarrow q^2}$|；⑤$\overrightarrow p$在基底{$\overrightarrow i$，$\overrightarrow j$，$\overrightarrow k$}下的坐标为（1，2，3），则在基底{$\overrightarrow i$+$\overrightarrow j$，$\overrightarrow j$+$\overrightarrow k$，$\overrightarrow k$+$\overrightarrow i$}下的坐标为（0，2，1）．
其中正确的是③⑤（把你认为正确的命题序号都填上）．
12．已知实数x，y满足logax+2logxa+logxy=4，其中常数a＞1，当y取最大值2时，对应的x的值为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网