题目内容
以下各数不能构成等差数列的是 ( )
| A.4,5,6 | B.1,4,7 |
C.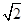 , ,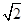 , ,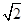 | D.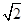 , ,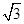 , , |
D
显然A,B,C选项中,给出的三数均能构成等差数列,故选D.事实上,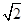 ,
,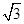 ,
, 不能构成等差数列,证明如下:假设
不能构成等差数列,证明如下:假设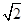 ,
,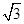 ,
, 成等差数列,则2
成等差数列,则2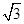 =
=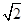 +
+ ?12=7+2
?12=7+2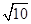 ?5=2
?5=2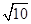 ?25=40.这是不可能的.
?25=40.这是不可能的.
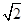 ,
,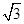 ,
, 不能构成等差数列,证明如下:假设
不能构成等差数列,证明如下:假设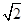 ,
,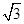 ,
, 成等差数列,则2
成等差数列,则2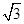 =
=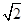 +
+ ?12=7+2
?12=7+2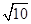 ?5=2
?5=2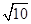 ?25=40.这是不可能的.
?25=40.这是不可能的.
练习册系列答案
相关题目
 <2.
<2. )=4x-
)=4x- +1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).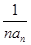 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.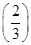 n}中的最大项是第k项,则k= .
n}中的最大项是第k项,则k= .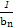 }的前n项和Tn.
}的前n项和Tn.