题目内容
(1)已知两个等比数列{an},{bn},满足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3,若数列{an}唯一,求a的值;
(2)是否存在两个等比数列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.
(2)是否存在两个等比数列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.
(1) a=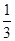 (2) 不存在,理由见解析
(2) 不存在,理由见解析
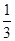 (2) 不存在,理由见解析
(2) 不存在,理由见解析解:(1)设等比数列{an}的公比为q,
则b1=1+a,b2=2+aq,b3=3+aq2,
由b1,b2,b3成等比数列,得(2+aq)2=(1+a)(3+aq2),
即aq2-4aq+3a-1=0,(*)
由a>0得Δ=4a2+4a>0,故方程(*)有两个不同的实数根,
再由{an}唯一,知方程(*)必有一根为0,将q=0代入方程(*)得a=
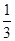 .
.(2)假设存在两个等比数列{an},{bn}使b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列,设等比数列{an}的公比为q1,等比数列{bn}的公比为q2,
则b2-a2=b1q2-a1q1,
b3-a3=b1
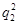 -a1
-a1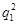 ,
,b4-a4=b1
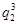 -a1
-a1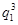 ,
,∵b1-a1,b2-a2,b3-a3,b4-a4成等差数列,得

即
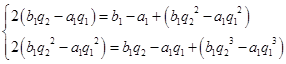
即
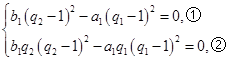
①×q2-②得a1(q1-q2)(q1-1) 2=0,
由a1≠0得q1=q2或q1=1.
(ⅰ)当q1=q2时由①②得b1=a1或q1=q2=1,
这时(b2-a2)-(b1-a1)=0与公差不为0矛盾.
(ⅱ)当q1=1时,由①②得b1=0或q2=1,
这时(b2-a2)-(b1-a1)=0与公差不为0矛盾.
综上所述,不存在两个等比数列{an}{bn}使b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
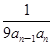 (n≥2),b1=
(n≥2),b1=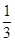 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.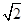 ,
,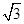 ,
,
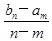 ;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.
;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.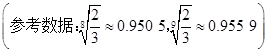
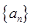 中,已知
中,已知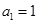 ,
,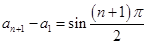 ,记
,记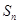 为数列
为数列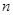 项和,则
项和,则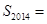 ( )
( )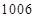
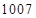

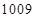
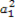 +
+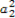 +
+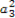 +…+
+…+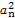 等于( )
等于( ) (2n-1)2
(2n-1)2