题目内容
若数列{n(n+4)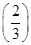 
n}中的最大项是第k项,则k= .
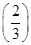n}中的最大项是第k项,则k= .4
法一 设数列为{an},则
an+1-an="(n+1)(n+5)"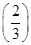n+1-n(n+4)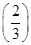n
=n[
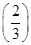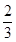(n2+6n+5)-n2-4n]
=
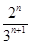(10-n2),
所以当n≤3时,an+1>an,即a1<a2<a3<a4,
当n≥4时,an+1<an,因此,a4>a5>a6>…,故a4最大,所以k=4.
法二 由题意得
化简得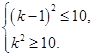
又∵k∈N*,∴k=4.
an+1-an="(n+1)(n+5)"
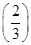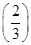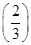n+1-n(n+4)n=
n[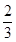(n2+6n+5)-n2-4n]=
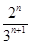(10-n2),所以当n≤3时,an+1>an,即a1<a2<a3<a4,
当n≥4时,an+1<an,因此,a4>a5>a6>…,故a4最大,所以k=4.
法二 由题意得
化简得
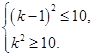
又∵k∈N*,∴k=4.
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
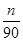(21n－n2－5)(n＝1，2，…，12)，按此预测，在本年度内，需求量超过1.5万件的月份是________．
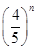Sn，是否存在正整数m，对一切正整数n，总有Tn≤Tm？若存在，求m的值；若不存在，说明理由．
+
+…+
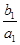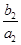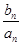=1-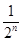
,n∈N* ,求{bn}的前n项和Tn.
，
，
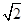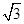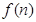个小正方形．则
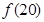等于( )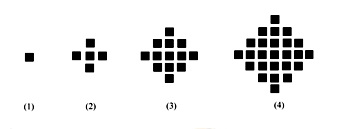
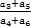的值为( )
