题目内容
14.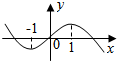 已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
分析 先求出函数f(x)的单调区间,将求不等式xf′(x)<0的解集转化为求不等式x(x-1)(x+1)<0的解集即可.
解答 解:由题意得:函数f(x)在(-∞,-1),(1,+∞)递减,在(-1,1)递增,
∴f′(x)=3ax2+2bx+c=3a(x-1)(x+1),
∴求不等式xf′(x)<0的解集,即为求不等式x(x-1)(x+1)<0的解集,
解得:-1<x<0或x>1,
故答案为:(-1,0)∪(1,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用,解不等式问题,是一道基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.随着移动互联网的深入普及,用手机上网的人数日益增多,某教育部门成立了调查小组,调查“常上网与高度近视的关系”,对某校高中二年级800名学生进行检查,得到如下2×2列联表:
根据列联表的数据,计算得到K2≈7.524,则( )
| 不常上网 | 常上网 | 总计 | |
| 不高度近视 | 70 | 150 | 220 |
| 高度近视 | 130 | 450 | 580 |
| 总计 | 200 | 600 | 800 |
| A. | 有99.5%的把握认为常上网与高度近视有关 | |
| B. | 有99.5%的把握认为常上网与高度近视无关 | |
| C. | 有99%的把握认为常上网与高度近视有关 | |
| D. | 有99%的把握认为常上网与高度近视无关 |
9.三位男生和一位女生并排照相,若女生不排在两端,则不同的排法共有( )
| A. | 6种 | B. | 12种 | C. | 18种 | D. | 24种 |