题目内容
5.已知函数f(x)=x3-3x,x∈R.(Ⅰ)判断函数y=f(x)在区间(0,1)和(1,+∞)上的单调性,并证明你的结论;
(Ⅱ)如果函数g(x)=x2-$\frac{k}{x}$-3,k∈R有三个零点,求实数k的取值范围.
分析 (Ⅰ)根据函数单调性的定义进行证明即可;
(Ⅱ)问题转化为函数f(x)=x3-3x与y=k有3个不同的交点的问题,求出函数f(x)的最大值和最小值,从而求出k的范围.
解答 解:(Ⅰ)函数f(x)在(0,1)递减,(1,+∞)递增,
证明如下:
f(x1)-f(x2)=(${{x}_{1}}^{3}$-3x1)-(${{x}_{2}}^{3}$-3x2)
=(${{x}_{1}}^{3}$-${{x}_{2}}^{3}$)-(3x1-3x2)
=(x1-x2)(${{x}_{1}}^{2}$+x1x2+${{x}_{2}}^{2}$-3),
设x1,x2∈(0,1),且x1<x2,
则x1-x2<0,0<${{x}_{1}}^{2}$<1,0<${{x}_{2}}^{2}$<1,0<x2x1<1,
${{x}_{1}}^{2}$+x1x2+${{x}_{2}}^{2}$-3<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴函数y=f(x)在区间(0,1)上是减函数,
设x1,x2∈(1,+∞),且x1<x2,
则x1-x2<0,${{x}_{1}}^{2}$>1,${{x}_{2}}^{2}$>1,x2x1>1,
${{x}_{1}}^{2}$+x1x2+${{x}_{2}}^{2}$-3>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数y=f(x)在区间(1,+∞)上是增函数,
综上,f(x)在(0,1)递减,在(1,+∞)递增;
(Ⅱ)∵函数g(x)有3个不同的零点,
∴方程x2-$\frac{k}{x}$-3=0有3个不同的实数根,
即方程x3-3x-k=0有3个不同的实数根,
∴函数f(x)=x3-3x与y=k有3个不同的交点,
由(Ⅰ)得:函数f(x)在区间(0,1)递减,在(1,+∞)递增,
∴f(x)在区间(0,+∞)的最小值是f(1)=-2,
∵f(-x)=(-x)3-3(-x)=-x3+3x=-f(x),
∴函数f(x)是奇函数,
∴函数f(x)在区间(-∞,0)上有最大值f(-1)=2,
∴当0<k<2或-2<k<0时,直线y=k和函数f(x)d的图象有3个不同的交点,
∴k的范围是(-2,0)∪(0,2).
点评 本题考查了函数的单调性的证明问题,函数的极值问题,考查函数的零点问题,考查导数的应用,是一道中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{3}{2}$-$\frac{1}{2}$i |
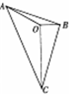 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.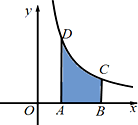 如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)
如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)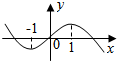 已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).