题目内容
19.在空间直角坐标系O-xyz中,已知P1(2,4,6),点P(1,3,-5)关于平面xOy对称的点为P2,则|P1P2|=$\sqrt{3}$.分析 先求出点P关于坐标平面的对称点,进而即可求出向量的坐标及模.
解答 解:∵点P(1,3,-5)关于xoy平面的对称点P2(1,3,5),
∴$\overrightarrow{{P}_{1}{P}_{2}}$=(-1,1,-1),
∴|P1P2|=$\sqrt{1+1+1}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查空间点当坐标的表示,空间距离的求法,熟练掌握向量的模的求法是解题的关键.

练习册系列答案
相关题目
11.两个数2和8的等差中项是( )
| A. | 5 | B. | -5 | C. | 10 | D. | 0 |
4.设F1和F2是双曲线$\left\{\begin{array}{l}x=2secθ\\ y=tanθ\end{array}\right.(θ为$为参数)的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,那么△F1PF2的面积是( )
| A. | 1 | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | 5 |
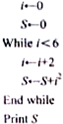 已知某程序伪代码如图,则输出结果S=56.
已知某程序伪代码如图,则输出结果S=56.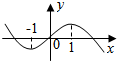 已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).