题目内容
4.已知cosx=-$\frac{{2\sqrt{5}}}{5},x∈(π,\frac{3}{2}π)$(Ⅰ) 求sin2x的值;
(Ⅱ) 求$tan(x+\frac{π}{4})$的值.
分析 (Ⅰ)由条件利用同角三角函数的基本关系求得sinx的值,再利用二倍角公式求得sin2x的值.
(Ⅱ)由(Ⅰ)求得tanx的值,再利用两角和的正切公式,求得$tan(x+\frac{π}{4})$的值.
解答 解:(Ⅰ) 因为$cosx=-\frac{{2\sqrt{5}}}{5},x∈(π,\frac{3}{2}π)$,所以sinx<0,
由sin2x+cos2x=1,得$sinx=-\frac{{\sqrt{5}}}{5}$,
∴$sin2x=2sinxcosx=\frac{4}{5}$.
(Ⅱ)由(Ⅰ),得$tanx=\frac{sinx}{cosx}=\frac{1}{2}$,
所以$tan(x+\frac{π}{4})=\frac{{tanx+tan\frac{π}{4}}}{{1-tanxtan\frac{π}{4}}}=\frac{{\frac{1}{2}+1}}{{1-\frac{1}{2}}}=3$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式,两角和的正切公式,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
14.若△ABC中,a=2bcosC,且sin2B+sin2C=2sin2A,则该三角形一定为( )
| A. | 等腰直角三角形 | B. | 等腰钝角三角形 | ||
| C. | 等边三角形 | D. | 不存在这样的三角形 |
19.利用二分法求方程2x+2x-7=0在区间(1,3)内近似解的过程中取区间的中点2,则下一个有该方程实根的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (1,2)或(2,3) | D. | 不能确定 |
13.复数$\frac{1+2i}{1+i}$的共轭复数等于( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{3}{2}$-$\frac{1}{2}$i |
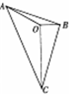 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.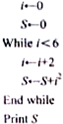 已知某程序伪代码如图,则输出结果S=56.
已知某程序伪代码如图,则输出结果S=56.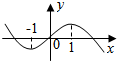 已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).