题目内容
20.已知$\overrightarrow{a}$是直线x+2y+1=0的一个方向向量,$\overrightarrow{b}$=(2,k),且$\overrightarrow{a}⊥\overrightarrow{b}$,则不等式|x-k|+|$\frac{3}{2}$k-x|>m2-3m-2恒成立的实数m的取值范围(-1,4).分析 求出直线的方向向量$\overrightarrow{a}$,根据$\overrightarrow{a}⊥\overrightarrow{b}$,得到k=4,结合绝对值不等式的性质将不等式恒成立进行转化求解即可.
解答 解:∵直线x+2y+1=0的斜率k=-$\frac{1}{2}$,$\overrightarrow{a}$是直线x+2y+1=0的一个方向向量,
∴$\overrightarrow{a}$=(1,$-\frac{1}{2}$),
∵$\overrightarrow{b}$=(2,k),且$\overrightarrow{a}⊥\overrightarrow{b}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=2-$\frac{1}{2}$k=0,
解得k=4,
则不等式等价为|x-4|+|6-x|>m2-3m-2恒成立,
∵|x-4|+|6-x|≥|x-4+6-x|=2,
∴m2-3m-2<2,
即m2-3m-4<0,
解得-1<m<4,
故答案为:(-1,4)
点评 本题主要考查不等式恒成立问题,考查直线的方向向量,向量垂直,绝对值不等式的性质以及一元二次不等式的解法,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
8.已知复数z=(a-2)+ai(a∈R,i为虚数单位)为纯虚数,则${∫}_{0}^{a}$$\sqrt{4-{x}^{2}}$dx的值为( )
| A. | π | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
15.在等差数列{an}的前n项和为Sn,若a1,a2,S3成等比数列,则$\frac{{S}_{n}}{n{a}_{n}}$等于( )
| A. | $\frac{n}{2n-1}$ | B. | $\frac{n}{2n+1}$ | C. | $\frac{2n-1}{n}$ | D. | $\frac{2n+1}{n}$ |
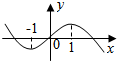 已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).