题目内容
3.已知等差数列{an}的前n项和Sn=n2+n+r,则r=0.分析 由题意可得a1,a2,a3,由数列{an}为等差数列可得r的方程,解方程可得.
解答 解:由题意可得a1=S1=12+1+r=2+r,
a2=S2-S1=(6+r)-(2+r)=4,
a3=S3-S2=(12+r)-(6+r)=6,
∵数列{an}为等差数列,
∴4×2=2+r+6,
解得r=0
故答案为:0
点评 本题考查等差数列的求和公式,属基础题.

练习册系列答案
相关题目
13.复数$\frac{1+2i}{1+i}$的共轭复数等于( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{3}{2}$-$\frac{1}{2}$i |
11.两个数2和8的等差中项是( )
| A. | 5 | B. | -5 | C. | 10 | D. | 0 |
4.设F1和F2是双曲线$\left\{\begin{array}{l}x=2secθ\\ y=tanθ\end{array}\right.(θ为$为参数)的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,那么△F1PF2的面积是( )
| A. | 1 | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | 5 |
8.已知复数z=(a-2)+ai(a∈R,i为虚数单位)为纯虚数,则${∫}_{0}^{a}$$\sqrt{4-{x}^{2}}$dx的值为( )
| A. | π | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
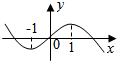 已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,若f′(x)是f(x)的导函数,则不等式xf′(x)<0的解集为(-1,0)∪(1,+∞).