题目内容
14.已知平面α,β,直线m,n,下列命题中不正确的是( )| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
分析 利用在与平面,直线与直线的平行与垂直的判定定理以及性质定理推出结果即可.
解答 解:若m⊥α,m⊥β,则α∥β,满足平面与平面平行的判定定理,所以A正确;
若m∥n,m⊥α,则n⊥α,满足满足直线与平面平行的性质,所以B正确;
若m⊥α,m?β,则α⊥β,满足平面与平面垂直的性质,所以C正确;
若m∥α,α∩β=n,则m∥n,也可能得到m,n是异面直线,所以D不正确.
故选:D.
点评 本题考查直线与直线,直线与平面,平面与平面平行与垂直的判断与性质,考查基本知识的应用.

练习册系列答案
相关题目
2. 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )| A. | [$\frac{54\sqrt{13}}{13}$,12$\sqrt{3}$] | B. | [$\frac{54\sqrt{13}}{13}$,9$\sqrt{3}$] | C. | [$\frac{48\sqrt{13}}{13}$,12$\sqrt{3}$] | D. | [$\frac{48\sqrt{13}}{13}$,3$\sqrt{39}$] |
 在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.
在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.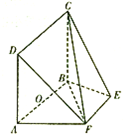 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.