Question

3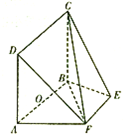．如图，等腰梯形ABEF中，AB∥EF，AB=2，AD=AF=1，AF⊥BF，O为AB的中点，矩形ABCD所在平面与平面ABEF互相垂直．
（1）求证：AF⊥平面CBF；
（2）在棱FC上是否存在M，使得OM∥平面DAF？
（3）求点A到平面BDF的距离．

Answer 1

分析 （1）欲证AF⊥平面CBF，根据直线与平面垂直的判定定理可知只需证AF与平面CBF内两相交直线垂直，根据面面垂直的性质可知CB⊥平面ABEF，而AF?平面ABEF，则AF⊥CB，而AF⊥BF，满足定理所需条件；
（2）M为FC的中点，OM∥平面DAF．欲证OM∥平面DAF，根据直线与平面平行的判定定理可知只需证OM与平面DAF内一直线平行即可，设DF的中点为N，则MNAO为平行四边形，则OM∥AN，又AN?平面DAF，OM不属于平面DAF，满足定理所需条件；
（3）过A做AH⊥DF于H，根据面面垂直的性质可知AH⊥平面BDF，AH为点A到平面BDF的距离，即可得出结论．

解答 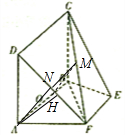（1）证明：∵平面ABCD⊥平面ABEF，CB⊥AB，
平面ABCD∩平面ABEF=AB
∴CB⊥平面ABEF，
∵AF?平面ABEF
∴AF⊥CB
又AF⊥BF，CB∩BF=B，
∴AF⊥平面CBF；
（2）M为FC的中点，OM∥平面DAF．
证明：设DF的中点为N，则MN平行且等于$\frac{1}{2}$CD
又AO平行且等于$\frac{1}{2}$CD．
∴MN平行且等于AO，
∴MNAO为平行四边形
∴OM∥AN，
又AN?平面DAF，OM不属于平面DAF
∴OM∥平面DAF；
（3）解：过A做AH⊥DF于H，
∵AD⊥平面ABEF，
∴AD⊥BF，
∵AF⊥BF，AD∩AF=A，
∴BF⊥平面ADF，
∴平面ADF⊥平面BDF，
∴AH⊥平面BDF，
∴AH为点A到平面BDF的距离．
在△ADF中，AD=AF=1，∴AH=$\frac{\sqrt{2}}{2}$．

点评 本题主要考查直线与平面平行的判定，以及直线与平面垂直的判定和A到平面BDF的距离的计算，考查学生分析解决问题的能力，属于中档题．