题目内容
4.已知等差数列{an}的前n项和为Sn,等比数列{bn}满足a1=b1=1,S3=b3+2,S5=b5-1.(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)如果数列{bn}为递增数列,求数列{anbn}的前n项和Tn.
分析 (1)利用等差数列、等比数列的通项公式,列出方程组,即可求出数列的通项;
(2)利用错位相减法,即可求数列{anbn}的前n项和为Sn
解答 解:(1)∵等比数列{bn}满足a1=b1=1,S3=b3+2,S5=b5-1.
∴$\left\{\begin{array}{l}{\frac{3(1+1+2d)}{2}={q}^{2}+2}\\{\frac{5(1+1+4d)}{2}={q}^{4}-1}\end{array}\right.$
解得q2=4,q2=$-\frac{2}{3}$(舍去)d=1,
q=±2,
当q=2时,an=1+n-1=n,bn=2n-1,
当q=-2时,an=1+n-1=n,bn=($\frac{1}{2}$)n-1=21-n
(2)∵数列{bn}为递增数列,
∴bn=2n-1,an=n.
∴anbn=n•2n-1.
∵前n项和Tn=1×20+2×21+3×22+4×23+…+(n-1)•2n-2+n•2n-1.①
2Tn=1•21+2×22+3×23+…+(n-1)•2n-1+n•2n,②
①-②:-Tn=1+2n-1-n•2n=(2+22+…+2n-1)-n•2n.
Tn=1-2n+n•2n
点评 本题考查等差数列与等比数列的基本关系式,考查错位相减法的应用,考查计算能力,属于中档题,计算准确.

练习册系列答案
相关题目
14.已知平面α,β,直线m,n,下列命题中不正确的是( )
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
9.设函数f(x)=sin(2x-$\frac{π}{2}$)(x∈R),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
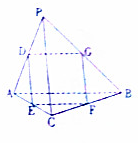 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.