Question

【题目】已知函数y=f（x）是定义域为R的偶函数． 当x≥0时，f（x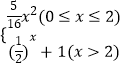）= ，若关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且仅有6个不同实数根，则实数a的取值范围是 ．

Answer 1

【答案】（﹣ ，﹣ ）∪（﹣ ，﹣1）
【解析】解：依题意f（x）在（﹣∞，﹣2）和（0，2）上递增，在（﹣2，0）和（2，+∞）上递减，
当x=±2时，函数取得极大值 ；
当x=0时，取得极小值0．
要使关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且只有6个不同实数根，
设t=f（x），
则t2+at+b=0必有两个根t1、t2 ，
则有两种情况符合题意：
1）t1= ，且t2∈（1， ），
此时﹣a=t1+t2 ，
则a∈（﹣ ，﹣ ）；
2）t1∈（0，1]，t2∈（1， ），
此时同理可得a∈（﹣ ，﹣1），
综上可得a的范围是（﹣ ，﹣ ）∪（﹣ ，﹣1）．
所以答案是：（﹣ ，﹣ ）∪（﹣ ，﹣1）．