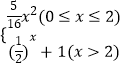题目内容
【题目】已知函数 ![]() .
.
(1)当a<0时,若x>0,使f(x)≤0成立,求a的取值范围;
(2)令g(x)=f(x)﹣(a+1)x,a∈(1,e],证明:对x1 , x2∈[1,a],恒有|g(x1)﹣g(x2)|<1.
【答案】
(1)解:当a<0,由 ![]() .
.
令f′(x)=0,
∴ ![]()
列表:
x |
|
|
|
f′(x) | ﹣ | 0 | + |
f(x) | 减函数 | 极小值 | 增函数 |
这是 ![]() .
.
∵x>0,使f(x)≤0成立,
∴ ![]() ,
,
∴a≤﹣e,
∴a范围为(﹣∞,﹣e].
(2)解:因为对x∈[1,a], ![]() ,所以g(x)在[1,a]内单调递减.所以
,所以g(x)在[1,a]内单调递减.所以 ![]() .
.
要证明|g(x1)﹣g(x2)|<1,
只需证明 ![]() <1,
<1,
即证明 ![]() <0.
<0.
令 ![]() ,
,
![]() >0,
>0,
所以 ![]() 在a∈(1,e]是单调递增函数,
在a∈(1,e]是单调递增函数,
所以 ![]() <0,
<0,
故命题成立
【解析】(1)求出函数f(x)的导函数,令导函数等于0求出根,列出x,f′(x),f(x)的情况变化表,通过表得到函数的最小值,令最小值小于等于0即可.(2)求出g(x)的导函数,判断出导函数的符号,得到函数g(x)递减,求出g(x)的最大值及最小值,通过分析法只需证得最大值与最小值差的绝对值小于1即可,构造新函数h(x),h(x)的导函数,判断出其符号,进一步求出h(x)的最大值,得证.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目