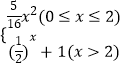Question

【题目】已知函数，记不等式f（x）≤4的解集为M，记函数的定义域为集合N．

（Ⅰ）求集合M和N；

（Ⅱ）求M∩N和M∪(RN)．

Answer 1

【答案】（1）{x|﹣≤x≤3}； （2）{x|x≤1或x＞3}.

【解析】

Ⅰ）利用分类讨论法求出f（x）≤4的解集M和g（x）的定义域N；

（Ⅱ）根据集合的运算法则求出M∩N和M∪RN的值．

函数，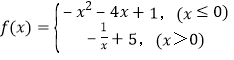

当x≤0时，f（x）=﹣x2﹣4x+1≤4，即x2+4x+3≥0，

解得x≤﹣3或﹣1≤x≤0，

当x＞0时，f（x）=﹣+5≤4，解得0＜x≤1；

综上，不等式f（x）≤4的解集M={x|x≤﹣3或﹣1≤x≤1}；

∵函数g（x）=的定义域为集合N，

∴N={x|﹣2x2+5x+3≥0}={x|﹣≤x≤3}；

（Ⅱ）由题意知，M∩N={x|﹣≤x≤1}，

RN={x|x＜﹣或x＞3}，

∴M∪RN={x|x≤1或x＞3}．