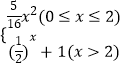题目内容
【题目】如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF= ![]() km,FE=3km,EC=
km,FE=3km,EC= ![]() km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=
km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y= ![]() (其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分. 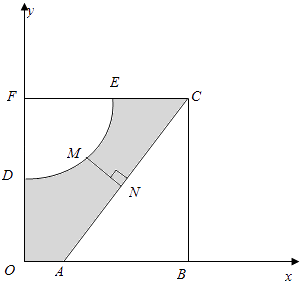
(1)求a,b,k,m的值;
(2)现准备建一座桥MN,其中M,N分别在DE,AC上,且MN⊥AC,设点M的横坐标为t.
①请写出桥MN的长l关于t的函数关系式l=f(t),并注明定义域;
②当t为何值时,l取得最小值?最小值是多少?
【答案】
(1)解:由题意得:OD=BC=4,OB=FC,
∴D(0, ![]() ),E(3,4),A(
),E(3,4),A( ![]() ,0),C(
,0),C( ![]() ,4),
,4),
把D(0, ![]() ),E(3,4)代入y=
),E(3,4)代入y= ![]()
得: 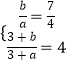 ,解得:a=﹣4,b=﹣7,
,解得:a=﹣4,b=﹣7,
把A( ![]() ,0),C(
,0),C( ![]() ,4)代入y=kx+m
,4)代入y=kx+m
得: 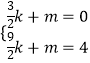 ,解得:k=
,解得:k= ![]() ,m=﹣2
,m=﹣2
(2)解:由(1)得:M点在y= ![]() 上,
上,
∴M(t, ![]() ),t∈[0,3],
),t∈[0,3],
①桥MN的长l为MN到直线y= ![]() x﹣2的距离,
x﹣2的距离,
故l=f(x)= ![]() =
= ![]() |4t+
|4t+ ![]() ﹣9|,t∈[0,3];
﹣9|,t∈[0,3];
②由①得:f(t)= ![]() |4t+
|4t+ ![]() ﹣9|=
﹣9|= ![]() |4(t﹣4)+
|4(t﹣4)+ ![]() +7|,
+7|,
而t﹣4<0, ![]() <0,
<0,
∴4(t﹣4)+ ![]() ≤﹣2
≤﹣2 ![]() =﹣12,
=﹣12,
当且仅当4(t﹣4)= ![]() 时即t=
时即t= ![]() “=”成立,
“=”成立,
∴f(t)min= ![]() |﹣12+7|=1
|﹣12+7|=1
【解析】(1)先求出D、E、A、C点的坐标,代入函数的解析式,从而求出a,b,k,m的值即可;(2)①先表示出M点的坐标,问题转化为求M到直线AC的距离即可;②由基本不等式的性质求出最小值即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案