题目内容
【题目】考察![]() 所有排列,将每种排列视为一个
所有排列,将每种排列视为一个![]() 元有序实数组
元有序实数组![]() ,设
,设![]() 且
且![]() ,设
,设![]() 为
为![]() 的最大项,其中
的最大项,其中![]() .记数组
.记数组![]() 为
为![]() .例如,
.例如,![]() 时,
时,![]() ;
;![]() 时,
时,![]() .若数组
.若数组![]() 中的不同元素个数为2.
中的不同元素个数为2.
(1)若![]() ,求所有
,求所有![]() 元有序实数组
元有序实数组![]() 的个数;
的个数;
(2)求所有![]() 元有序实数组
元有序实数组![]() 的个数.
的个数.
【答案】(1)11;(2)![]()
【解析】
(1)数组![]() 中的不同元素个数为2,故
中的不同元素个数为2,故![]() 为1,2,3中的的任意一个,根据4的位置讨论即可得到有序实数组
为1,2,3中的的任意一个,根据4的位置讨论即可得到有序实数组![]() 的个数;
的个数;
(2)数组![]() 中的不同元素个数为2,
中的不同元素个数为2,![]() 为1,2,
为1,2,![]() 中的的任意一个,则数
中的的任意一个,则数![]() ,
,![]() 只能在
只能在![]() 之后,而在
之后,而在![]() 和
和![]() 之间只能出现1,2,
之间只能出现1,2,![]() 中的某些数,设
中的某些数,设![]() ,根据计数原理以及排列组合知识即可得到当
,根据计数原理以及排列组合知识即可得到当![]() 时,数组
时,数组![]() 的个数,进而当
的个数,进而当![]() 从1变化到
从1变化到![]() 时,即可求出
时,即可求出![]() 元有序实数组
元有序实数组![]() 的全部个数.
的全部个数.
(1)因为数组![]() 中的不同元素个数为2,
中的不同元素个数为2,
所以![]() 为1,2,3中的任意一个,即4只能为
为1,2,3中的任意一个,即4只能为![]() 或
或![]() 或
或![]() .
.
当![]() 时,则
时,则![]() 是1,2,3的任意一个排列,总数有
是1,2,3的任意一个排列,总数有![]() 个;
个;
当![]() 时,则
时,则![]() 是1,2,3的一个排列,且
是1,2,3的一个排列,且![]() ,故
,故![]() 为
为![]() 或
或![]() 或
或![]() ,总数有3个;
,总数有3个;
当![]() 时,则
时,则![]() 是1,2,3,的任意一个排列,且
是1,2,3,的任意一个排列,且![]() ,故
,故![]() 为
为![]() 或
或![]() ,总数有2个;
,总数有2个;
综上,有序实数组![]() 的个数为
的个数为![]() ,
,
(2)因为数组![]() 中的不同元素个数为2,
中的不同元素个数为2,
所以![]() 为
为![]() 中的任意一个.
中的任意一个.
当![]() 时,数
时,数![]() 在
在![]() 中必须位于
中必须位于![]() 之后,而在
之后,而在![]() 与
与![]() 之间只能出现
之间只能出现![]() 中的某些数,所以
中的某些数,所以![]() 只能作
只能作![]() 出现.
出现.
当![]() 时,
时,![]() 可为从
可为从![]() 中任意选出
中任意选出![]() 个元素的排列,而
个元素的排列,而![]() 则为其余
则为其余![]() 个元素的全排列.所以与
个元素的全排列.所以与![]() 相对应的排列个数为:
相对应的排列个数为: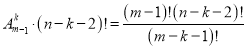 .
.
所以所有![]() 元有序实数组
元有序实数组![]() 的个数记为
的个数记为![]() ,
,
则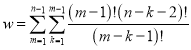
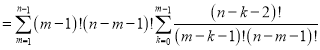
![]()
![]()

练习册系列答案
相关题目