题目内容
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
【答案】(1) 不变化;(2)![]() ;(3)先派甲,再派乙,最后派丙时, 均值(数字期望)达到最小
;(3)先派甲,再派乙,最后派丙时, 均值(数字期望)达到最小
【解析】
(1)按甲在先,乙次之,丙最后的顺序派人,任务能被完成的概率为![]()
![]() .
.
若甲在先,丙次之,乙最后的顺序派人,任务能被完成的概率为![]()
![]() ,
,
发现任务能完成的概率是一样.
同理可以验证,不论如何改变三个人被派出的先后顺序,任务能被完成的概率不发生变化.
(2)由题意得![]() 可能取值为
可能取值为![]()
∴![]() ,
,
∴其分布列为:
|
|
|
|
|
|
|
|
![]() .
.
(3)![]() ,
,![]()
∴要使所需派出的人员数目的均值(数字期望)达到最小,
则只能先派甲、乙中的一人.
∴若先派甲,再派乙,最后派丙,则![]() span>;
span>;
若先派乙,再派甲,最后派丙, 则![]() ,
,
![]() ,
,
∴先派甲,再派乙,最后派丙时, 均值(数字期望)达到最小.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑.某企业为了参加这次盛会,提升行业竞争力,加大了科技投入.该企业连续6年来的科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 | 5.6 | 6.5 | 12.0 | 27.5 | 80.0 | 129.2 |
并根据数据绘制散点图如图所示:
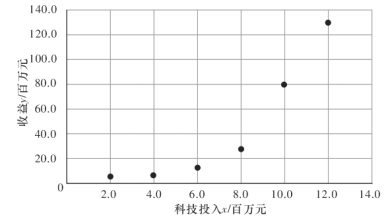
根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
|
|
|
|
|
|
43.5 | 4.5 | 854.0 | 34.7 | 12730.4 | 70 |
其中![]() ,
,![]() .
.
(1)(i)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(ii)根据所建立的回归方程,若该企业想在下一年收益达到2亿,则科技投入的费用至少要多少?(其中![]() )
)
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两人所建立的模型,谁的拟合效果更好.
,试比较甲乙两人所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为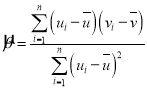 ,
,![]() ,相关指数:
,相关指数: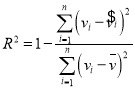 .
.