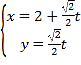题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 有两个零点,求a的取值范围;
有两个零点,求a的取值范围;
(2)设函数![]() 的两个零点为
的两个零点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)函数![]() 有两个零点,等价于函数
有两个零点,等价于函数![]() 的图象与直线
的图象与直线![]() 有两个交点,求
有两个交点,求![]() ,判断
,判断![]() 的单调性,从而求出a的取值范围;
的单调性,从而求出a的取值范围;
(2)不妨设![]() ,由题意
,由题意![]() ,可得
,可得![]() ,两式相减,可得
,两式相减,可得![]() ,两式相加可得
,两式相加可得![]() .问题转化为求函数
.问题转化为求函数![]() 的单调性,根据当
的单调性,根据当![]() 时,
时,![]() ,得到
,得到![]() ,从而证明结论.
,从而证明结论.
(1)函数![]() 的定义域为
的定义域为![]() ,函数
,函数![]() 有两个零点,即方程
有两个零点,即方程![]() 有两个根,
有两个根,
令![]() ,则函数
,则函数![]() 的图象与直线
的图象与直线![]() 有两个交点.
有两个交点.
![]() ,令
,令![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
![]() 函数
函数![]() 的图象与直线
的图象与直线![]() 有两个交点时,
有两个交点时,![]() ,
,
即函数![]() 有两个零点时,a的取值范围为
有两个零点时,a的取值范围为![]() .
.
(2)证明:不妨设![]() .
.
由题意可得![]() .
.
两式相减可得![]() ,两式相加可得
,两式相加可得![]() .
.
![]()
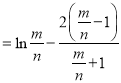 .
.
令![]() ,则
,则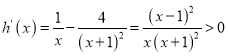 ,
,
![]() 函数
函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() .
.
![]() .
.
又![]() ,
,
![]() ,即
,即![]() ,
,
![]() .
.

练习册系列答案
相关题目
【题目】新能源汽车正以迅猛的势头发展,越来越多的企业不断推出纯电动产品,某汽车集团要对过去一年推出的四款纯电动车型中销量较低的![]() 车型进行产品更新换代.为了了解这种车型的外观设计是否需要改进,该集团委托某调查机构对大众做问卷调查,并从参与调查的人群中抽取了
车型进行产品更新换代.为了了解这种车型的外观设计是否需要改进,该集团委托某调查机构对大众做问卷调查,并从参与调查的人群中抽取了![]() 人进行抽样分析,得到如下表格:(单位:人)
人进行抽样分析,得到如下表格:(单位:人)
喜欢 | 不喜欢 | 合计 | |
青年人 |
|
|
|
中年人 |
|
|
|
合计 |
|
|
|
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为大众对
的前提下认为大众对![]() 型车外观设计的喜欢与年龄有关?
型车外观设计的喜欢与年龄有关?
(2)现从所抽取的中年人中按是否喜欢![]() 型车外观设计利用分层抽样的方法抽取
型车外观设计利用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送五折优惠券,求选出的
人赠送五折优惠券,求选出的![]() 人中至少有
人中至少有![]() 人喜欢该集团
人喜欢该集团![]() 型车外观设计的概率;
型车外观设计的概率;
(3)将频率视为概率,从所有参与调查的人群中随机抽取![]() 人赠送礼品,记其中喜欢
人赠送礼品,记其中喜欢![]() 型车外观设计的人数为
型车外观设计的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: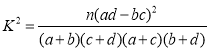 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|