题目内容
【题目】某工厂生产一种产品的标准长度为![]() ,只要误差的绝对值不超过
,只要误差的绝对值不超过![]() 就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
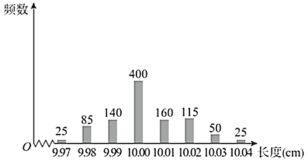
(1)估计该批次产品长度误差绝对值的数学期望;
(2)如果视该批次产品样本的频率为总体的概率,要求从工厂生产的产品中随机抽取2件,假设其中至少有1件是标准长度产品的概率不小于0.8时,该设备符合生产要求.现有设备是否符合此要求?若不符合此要求,求出符合要求时,生产一件产品为标准长度的概率的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据题意即可写出该批次产品长度误差的绝对值![]() 的频率分布列,再根据期望公式即可求出;
的频率分布列,再根据期望公式即可求出;
(2)由(1)可知,任取一件产品是标准长度的概率为0.4,即可求出随机抽取2件产品,都不是标准长度产品的概率,由对立事件的概率公式即可得到随机抽取2件产品,至少有1件是标准长度产品的概率,判断其是否符合生产要求;当不符合要求时,设生产一件产品为标准长度的概率为![]() ,可根据上述方法求出
,可根据上述方法求出![]() ,解
,解![]() ,即可得出最小值.
,即可得出最小值.
(1)由柱状图,该批次产品长度误差的绝对值![]() 的频率分布列为下表:
的频率分布列为下表:
| 0 | 0.01 | 0.02 | 0.03 | 0.04 |
频率 | 0.4 | 0.3 | 0.2 | 0.075 | 0.025 |
所以![]() 的数学期望的估计为
的数学期望的估计为
![]() .
.
(2)由(1)可知任取一件产品是标准长度的概率为0.4,设至少有1件是标准长度产品为事件![]() ,则
,则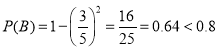 ,故不符合概率不小于0.8的要求.
,故不符合概率不小于0.8的要求.
设生产一件产品为标准长度的概率为![]() ,
,
由题意![]() ,又
,又![]() ,解得
,解得![]() ,
,
所以符合要求时,生产一件产品为标准长度的概率的最小值为![]() .
.

【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.