题目内容
已知函数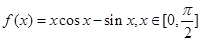 .
.
(1)求证: ;
;
(2)若 对
对 恒成立,求
恒成立,求 的最大值与
的最大值与 的最小值.
的最小值.
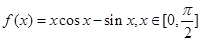 .
.(1)求证:
 ;
;(2)若
 对
对 恒成立,求
恒成立,求 的最大值与
的最大值与 的最小值.
的最小值.(1)详见解析;(2) 的最大值为
的最大值为 ,
, 的最小值为1.
的最小值为1.
 的最大值为
的最大值为 ,
, 的最小值为1.
的最小值为1.试题分析:(1)求
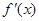 ,由
,由 ,判断出
,判断出 ,得出函数
,得出函数 在
在 上单调递减,从而
上单调递减,从而 ;(2)由于
;(2)由于 ,“
,“ ”等价于“
”等价于“ ”,“
”,“ ”等价于“
”等价于“ ”,令
”,令 ,则
,则 ,对
,对 分
分 ;
; ;
; 进行讨论,
进行讨论,用导数法判断函数
 的单调性,从而确定当
的单调性,从而确定当 对
对 恒成立时
恒成立时 的最大值与
的最大值与 的最小值.
的最小值.(1)由
 得
得 ,
,因为在区间
 上
上 ,所以,
,所以, 在区间
在区间 上单调递减,
上单调递减,从而
 .
.(2)当
 时,“
时,“ ”等价于“
”等价于“ ”,“
”,“ ”等价于“
”等价于“ ”,
”,令
 ,则
,则 ,
,当
 时,
时, 对任意
对任意 恒成立,
恒成立,当
 时,因为对任意
时,因为对任意 ,
, ,所以
,所以 在区间
在区间 上单调递减,从而
上单调递减,从而 对任意
对任意 恒成立.
恒成立.当
 时 ,存在唯一的
时 ,存在唯一的 使得
使得 ,
, 、
、 在区间
在区间 上的情况如下表:
上的情况如下表: |  |  |  |
 |  |  |  |
 |  | |  |
因为
 在区间
在区间 上是增函数,所以
上是增函数,所以 ,进一步“
,进一步“ 对任意
对任意 恒成立”
恒成立”,当且仅当
 ,即
,即 .
.综上所述,当且仅当
 时,
时, 对任意
对任意 恒成立.当且仅当
恒成立.当且仅当 时,
时, 对任意
对任意 恒成立.
恒成立.所以,若
 对
对 恒成立,则
恒成立,则 的最大值为
的最大值为 与
与 的最小值1.
的最小值1.
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 ,
, 。
。 在
在 上的值域;
上的值域; ,对
,对 ,
, 恒成立,
恒成立, 的取值范围
的取值范围 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).

 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围; 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由.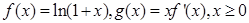 ,其中
,其中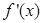 是
是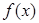 的导函数.
的导函数.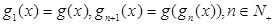 ,
,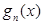 的表达式;
的表达式;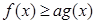 恒成立,求实数
恒成立,求实数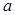 的取值范围;
的取值范围;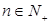 ,比较
,比较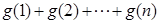 与
与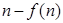 的大小,并加以证明.
的大小,并加以证明. 为常数,e=2.71828…是自然对数的底数),曲线
为常数,e=2.71828…是自然对数的底数),曲线 在点
在点 处的切线与x轴平行.
处的切线与x轴平行. 的单调区间;
的单调区间; ,其中
,其中 为
为 .
.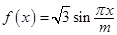 .若存在
.若存在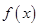 的极值点
的极值点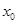 满足
满足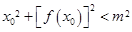 ,则m的取值范围是( )
,则m的取值范围是( )



 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围; ,
, ,
, ,其中
,其中 。
。 与
与 的图像在交点(2,
的图像在交点(2, )处的切线互相垂直,
)处的切线互相垂直, 的值;
的值; 是函数
是函数 的一个极值点,
的一个极值点, 和1是
和1是
 ,求
,求 ;
; 时,若
时,若 ,
, 是
是 -
- |
|
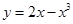 在横坐标为
在横坐标为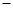 l的点处的切线为
l的点处的切线为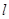 ,则直线
,则直线


