[题目]已知符号函数sgn(x)= .则函数f﹣lnx的零点个数为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知符号函数sgn（x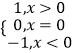）= ，则函数f（x）=sgn（lnx）﹣lnx的零点个数为．

【答案】3
【解析】解：①如果lnx＞0，即x＞1时，那么函数f（x）=sgn（lnx）﹣lnx转化为函数f（x）=1﹣lnx，令1﹣lnx=0，得x=e，
即当x＞1时．函数f（x）=sgn（lnx）﹣lnx的零点是e；
②如果lnx=0，即x=1时，
那么函数f（x）=sgn（lnx）﹣lnx转化为函数f（x）=0﹣lnx，令0﹣lnx=0，得x=1，
即当x=1时．函数f（x）=sgn（lnx）﹣lnx的零点是1；
③如果lnx＜0，即0＜x＜1时，
那么函数f（x）=sgn（lnx）﹣lnx转化为函数f（x）=﹣1﹣lnx，令﹣1﹣lnx=0，x= ，
即当0＜x＜1时．函数f（x）=sgn（lnx）﹣lnx的零点是；
综上函数f（x）=sgn（lnx）﹣lnx的零点个数为3．
所以答案是：3．

练习册系列答案

相关题目

【题目】如图所示，游乐场中摩天轮匀速逆时针旋转，每转一圈需要6min，其中心距离地面40.5m，摩天轮的半径为40m，已知摩天轮上点P的起始位置在最低点处，在时刻t（min）时点P距离地面的高度为f（t）=Asin（wt+φ）+h（A＞0，w＞0，﹣π＜φ＜0，t≥0）．
（1）求f（t）的单调区间；
（2）求证：f（t）+f（t+2）+f（t+4）是定值．

【题目】近几年，电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务，该配送站有8名新手快递员和4名老快递员，但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹，日工资320元；每个老快递员每天可配送300件包裹，日工资520元.

(Ⅰ)求该配送站每天需支付快递员的总工资最小值；

(Ⅱ)该配送站规定:新手快递员某个月被评为“优秀”，则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”，日工资会超过老快递员?

(参考数据: ，， .)

【题目】某校高三年级在高校自主招生期间，把学生的平时成绩按“百分制”折算并排序，选出前300名学生，并对这300名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列．（Ⅰ）请在图中补全频率分布直方图；
（Ⅱ）若B大学决定在成绩高的第4，5组中用
分层抽样的方法抽取6名学生，并且分成2组，每组3人
进行面试，求95分（包括95分）以上的同学被分在同一个小组的概率．

【题目】已知直线l1：2x+y+2=0，l2：mx+4y+n=0
（1）若l1⊥l2 ，求m的值，；
（2）若l1∥l2 ，且它们的距离为，求m、n的值．

【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数y与听课时间x（单位：分钟）之间的关系满足如图所示的图象，当x∈（0，12]时，图象是二次函数图象的一部分，其中顶点A（10，80），过点B（12，78）；当x∈[12，40]时，图象是线段BC，其中C（40，50）．根据专家研究，当注意力指数大于62时，学习效果最佳．
（1）试求y=f（x）的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由．

【题目】已知椭圆E：的左、右焦点分别为F1、F2 ，离心率，P为椭圆E上的任意一点（不含长轴端点），且△PF1F2面积的最大值为1．
（1）求椭圆E的方程；
（2）已知直x﹣y+m=0与椭圆E交于不同的两点A，B，且线AB的中点不在圆内，求m的取值范围．

【题目】已知圆C：x2+y2﹣2x﹣2ay+a2﹣24=0（a∈R）的圆心在直线2x﹣y=0上．
（1）求实数a的值；
（2）求圆C与直线l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）相交弦长的最小值．

【题目】如图，定义在[﹣1，5]上的函数f（x）由一段线段和抛物线的一部分组成．（Ⅰ）求函数f（x）的解析式；
（Ⅱ）指出函数f（x）的自变量x在什么范围内取值时，函数值大于0，小于0或等于0（不需说理由）．

试题分类