Question

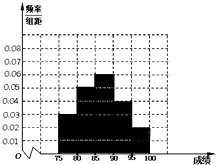
【题目】某校高三年级在高校自主招生期间，把学生的平时成绩按“百分制”折算并排序，选出前300名学生，并对这300名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列． （Ⅰ）请在图中补全频率分布直方图；
（Ⅱ）若B大学决定在成绩高的第4，5组中用
分层抽样的方法抽取6名学生，并且分成2组，每组3人
进行面试，求95分（包括95分）以上的同学被分在同一个小组的概率．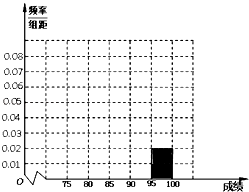

Answer 1

【答案】解：（Ⅰ）由频率分布直方图知， 第五组为：0.02×5×300=30人，
第五组、第一组、第四组、第二组、第三组的人数以次是一个以30为首项，总和为300的等差数列，
∴第五组、第一组、第四组、第二组、第三组的人数以次是30人，45人，60人，75人，90人．
∴绘制的频率分布直方图如右图所示；
（Ⅱ）第四组中抽取人数： 人，
第五组中抽取人数： 人，
∴两组共6人；
设第四组抽取的四人为A1 ， A2 ， A3 ， A4 ， 第五组抽取的2人为B1 ， B2 ，
这六人分成两组有两种情况，
情况一：B1 ， B2在同一小组：（A1 ， A2 ， A3），（A4 ， B1 ， B2）；（A1 ， A2 ， A4），（A3 ， B1 ， B2）；
（A1 ， A3 ， A4），（A2 ， B1 ， B2）；（A2 ， A3 ， A4），（A1 ， B1 ， B2），共有4种可能结果；
情况二：B1 ， B2不在同一小组：（B1 ， A1 ， A2），（B2 ， A3 ， A4）；（B1 ， A1 ， A3），（B2 ， A2 ， A4）；
（B1 ， A1 ， A4），（B2 ， A2 ， A3）；（B1 ， A2 ， A3），（B2 ， A1 ， A4）；
（B1 ， A2 ， A4），（B2 ， A1 ， A3）；（B1 ， A3 ， A4），（B2 ， A1 ， A2），共有6种可能结果；
两种情况总共10种可能结果，
∴两人被分在一组的概率为 ．
（另解：两人被分在一组的概率为 ）．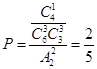

【解析】（Ⅰ）由频率分布直方图求出第五组的数据，再根据题意求出第一组、第四组、第二组、第三组的数据来，由此绘制频率分布直方图；（Ⅱ）根据分层抽样求出从第四、五组中抽取人数，组成样本，用列举法列出这六人分成两组的基本事件数，求出第五组中的2人被分在一组的概率即可． （另解：用排列与组合的方法求出两人被分在一组的概率也可）．
【考点精析】通过灵活运用频率分布直方图，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息即可以解答此题．