Question

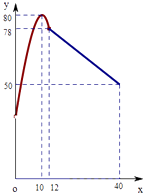
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数y与听课时间x（单位：分钟）之间的关系满足如图所示的图象，当x∈（0，12]时，图象是二次函数图象的一部分，其中顶点A（10，80），过点B（12，78）；当x∈[12，40]时，图象是线段BC，其中C（40，50）．根据专家研究，当注意力指数大于62时，学习效果最佳．
（1）试求y=f（x）的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由．

Answer 1

【答案】
（1）解：当x∈（0，12]时，

设f（x）=a（x﹣10）2+80

过点（12，78）代入得，

则

当x∈[12，40]时，

设y=kx+b，过点B（12，78）、C（40，50）

得 ，即y=﹣x+90

则的函数关系式为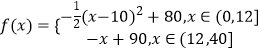

（2）解：由题意得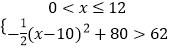， 或

得4＜x≤12或12＜x＜28，

4＜x＜28

则老师就在x∈（4，28）时段内安排核心内容，能使得学生学习效果最佳

【解析】（1）当x∈（0，12]时，设f（x）=a（x﹣10）2+80，把点（12，78）代入能求出解析式；当x∈[12，40]时，设y=kx+b，把点B（12，78）、C（40，50）代入能求出解析式．（2）由（1）的解析式，结合题设条件，列出不等式组，能求出老师就在什么时段内安排核心内容，能使得学生学习效果最佳
【考点精析】通过灵活运用函数的最值及其几何意义，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值即可以解答此题．