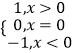题目内容
【题目】近几年,电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务,该配送站有8名新手快递员和4名老快递员,但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹,日工资320元;每个老快递员每天可配送300件包裹,日工资520元.
(Ⅰ)求该配送站每天需支付快递员的总工资最小值;
(Ⅱ)该配送站规定:新手快递员某个月被评为“优秀”,则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”,日工资会超过老快递员?
(参考数据: ![]() ,
, ![]() ,
, ![]() .)
.)
【答案】(1) 该配送站每天需支付快递员的总工资最小值为2560元;(2) 新手快递员至少连续5 个月被评为“优秀”,日工资会超过老快递员.
【解析】试题分析:(Ⅰ)本题属于线性规划问题,设安排新手快递员![]() 人,老快递员
人,老快递员![]() 人,可得约束条件和目标函数,画出可行域,经过平移直线
人,可得约束条件和目标函数,画出可行域,经过平移直线![]() 可得最优解为
可得最优解为![]() ,求得
,求得![]() 元。(Ⅱ) 设新手快递员连续
元。(Ⅱ) 设新手快递员连续![]() 个月被评为“优秀”,日工资会超过老员工,则由题意可得
个月被评为“优秀”,日工资会超过老员工,则由题意可得![]() .整理得
.整理得![]() ,两边取对数可解得
,两边取对数可解得![]() ,所以
,所以![]() 的最小值为5.
的最小值为5.
试题解析:
(Ⅰ)设安排新手快递员![]() 人,老快递员
人,老快递员![]() 人,
人,
由题意得 ,即
,即 ,
,
该配送站每天需支付快递员总工资为![]() .
.
作出不等式组表示的可行域如图所示.

作直线![]() ,平移直线
,平移直线![]() 可得到一组与之平行的直线
可得到一组与之平行的直线![]() .
.
由题设![]() 是可行域内的整点的横、纵坐标.
是可行域内的整点的横、纵坐标.
在可行域内的整点中,点![]() 使
使![]() 取得最小值,
取得最小值,
即当![]() 过点
过点![]() 时,
时, ![]() 取得最小值,且
取得最小值,且![]() (元).
(元).
即该配送站每天需支付快递员的总工资最小值为2560元
(Ⅱ)设新手快递员连续![]() 个月被评为“优秀”,日工资会超过老员工.
个月被评为“优秀”,日工资会超过老员工.
则由题意可得![]() .
.
整理得![]() ,
,
两边取对数可得![]() ,
,
所以![]()
![]() ,
,
又因为![]() ,所以
,所以![]() 的最小值为5.
的最小值为5.
即新手快递员至少连续5 个月被评为“优秀”,日工资会超过老快递员.

练习册系列答案
相关题目