Question

【题目】当实数m为何值时，复数z= +（m2﹣2m）i为
（1）实数？
（2）虚数？
（3）纯虚数？

Answer 1

【答案】
（1）解：z为实数，则虚部m2﹣2m=0，

可得 ，

解得m=2，

∴m=2时，z为实数．

（2）解：z为虚数，则虚部m2﹣2m≠0，且m≠0，

解得m≠2且m≠0．

当m≠2且m≠0时，z为虚数．

（3）解：z为纯虚数，则 ，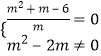

解得m=﹣3，

∴当m=﹣3时，z为纯虚数

【解析】（1）复数是实数，则虚部为零，求得m的实数值；（2）复数是虚数，则虚部不为零，可求得m的实数值；（3）复数是纯虚数，则实部为零，虚部不为零，即可求得m的实数值．
【考点精析】利用复数的定义对题目进行判断即可得到答案，需要熟知形如的数叫做复数，和分别叫它的实部和虚部．