题目内容
【题目】在矩形ABCD中，对角线AC与相邻两边所成的角为α，β，则cos2α+cos2β=1．类比到空间中一个正确命题是：在长方体ABCD﹣A1B1C1D1中，对角线AC1与相邻三个面所成的角为α，β，γ，则有 ．
【答案】cos2α+cos2β+cos2γ=2
【解析】解：我们将平面中的两维性质，类比推断到空间中的三维性质．
由在长方形中，设一条对角线与其一顶点出发的两条边所成的角分别是α，β，
则有cos2α+cos2β=1，
我们根据长方体性质可以类比推断出空间性质，
∵长方体ABCD﹣A1B1C1D1中，
对角线AC1与过A点的三个面ABCD，AA1B1B、AA1D1D所成的角分别为α，β，γ，
∴cosα= 
，cosβ= 
，cosγ= 
，
∴cos2α+cos2β+cos2γ
= 
=2．
所以答案是：cos2α+cos2β+cos2γ=2．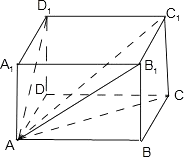
【考点精析】认真审题，首先需要了解类比推理(根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理)．
练习册系列答案
相关题目
